【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

参考答案:
【答案】15°
【解析】∵BD、CD分别平分∠ABC、∠ACB,∠A=60°,
∴∠DBC=![]() ∠ABC,∠DCB=
∠ABC,∠DCB=![]() ∠ACB,
∠ACB,
∴∠DBC+∠DCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=
(180°-∠A)=![]() ×(180°-60°)=60°,
×(180°-60°)=60°,
∴∠MBC+∠NCB=360°-60°=300°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠5+∠6=![]() ∠MBC,∠1=
∠MBC,∠1=![]() ∠NCB,
∠NCB,
∴∠5+∠6+∠1=![]() (∠NCB+∠NCB)=150°,
(∠NCB+∠NCB)=150°,
∴∠E=180°-(∠5+∠6+∠1)=180°-150°=30°,
∵BF、CF分别平分∠EBC、∠ECQ,
∴∠5=∠6,∠2=∠3+∠4,
∵∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,
即∠2=∠5+∠F,2∠2=2∠5+∠E,
∴2∠F=∠E,
∴∠F=![]() ∠E=
∠E=![]() ×30°=15°.
×30°=15°.
故答案是:15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中, BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若
 ,
,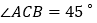 ,求∠D的度数;
,求∠D的度数;(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形的两条直角边分别为
 、
、
 ,斜边为
,斜边为 .我国古代数学家赵爽用四个这样的直角三角形拼成了如图的正方形,
.我国古代数学家赵爽用四个这样的直角三角形拼成了如图的正方形,(1)探究活动:如图1,中间围成的小正方形的边长为 (用含有
 、
、 的代数式表示);
的代数式表示);(2)探究活动:如图1,用不同的方法表示这个大正方形的面积,并写出你发现的结论;

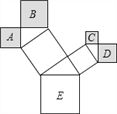
图1 图2
(3)新知运用:根据你所发现的结论完成下列问题.
①某个直角三角形的两条直角边
 、
、 满足式子
满足式子 ,求它的斜边
,求它的斜边 的值;
的值;②由①中结论,此三角形斜边
 上的高为 .
上的高为 .③如图2,这个勾股树图形是由正方形和直角三角形组成的,若正方形
 、
、 、
、 、
、 的面积分别为
的面积分别为 ,4,
,4,  ,
,  .则最大的正方形
.则最大的正方形 的边长是 .
的边长是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为( )
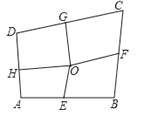
A. 6 B. 7 C. 8 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
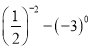 ;(2)
;(2) 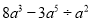
(3)
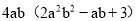 ;(4)
;(4)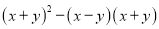
-
科目: 来源: 题型:
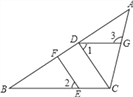
查看答案和解析>>【题目】如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a-2)0=1,则a的取值范围是___________.
相关试题

