【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.

(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1) 详见解析;(2)![]() .
.
【解析】试题分析:(1) 连接OC,由已知条件易得∠CAD=∠OCA,∠OCA=∠OAC,所以∠CAD=∠CAO,即可得AC平分∠DAB;(2).连接BE交OC于点H,易证OC⊥BE,可知∠OCA=∠CAD,因COS∠HCF=![]() ,可设HC=4,FC=5,则FH=3.由△AEF∽△CHF,设EF=3x,则AF=5x,AE=4x,所以OH=2x ,在△OBH中,由勾股定理列方程求解即可.
,可设HC=4,FC=5,则FH=3.由△AEF∽△CHF,设EF=3x,则AF=5x,AE=4x,所以OH=2x ,在△OBH中,由勾股定理列方程求解即可.
试题解析:(1)证明:连接OC,则OC⊥CD,
又AD⊥CD,
∴AD∥OC,
∴∠CAD=∠OCA,
又OA=OC,∴∠OCA=∠OAC,
∴∠CAD=∠CAO,
∴AC平分∠DAB.
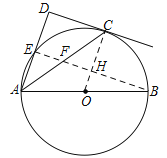
(2)解:连接BE交OC于点H,易证OC⊥BE,可知∠OCA=∠CAD,
∴COS∠HCF=![]() ,设HC=4,FC=5,则FH=3.
,设HC=4,FC=5,则FH=3.
又△AEF∽△CHF,设EF=3x,则AF=5x,AE=4x,∴OH=2x
∴BH=HE=3x+3 OB=OC=2x+4
在△OBH中,(2x)2+(3x+3)2=(2x+4)2
化简得:9x2+2x-7=0,解得:x=![]() (另一负值舍去).
(另一负值舍去).
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边长分别为a,b,c,且(a-c)∶(a+b)∶(c-b)=-2∶7∶1,则△ABC是( )
A. 等腰三角形 B. 等边三角形
C. 直角三角形 D. 等腰直角三角形
-
科目: 来源: 题型:
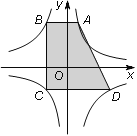
查看答案和解析>>【题目】如图,A、C为反比例函数
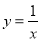 上两点,B、D为反比例函数
上两点,B、D为反比例函数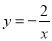 上两点,且AB⊥
上两点,且AB⊥ 轴,BC⊥
轴,BC⊥ 轴,CD⊥
轴,CD⊥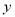 轴,点A的横坐标为
轴,点A的横坐标为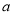 (
(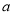 >0).
>0).(1)试用
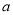 直接表示点A、B、C、D的坐标.
直接表示点A、B、C、D的坐标.(2)求四边形ABCD的边长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形的两边长分别为3和4,则第三边的长不可能的是( )
A. 2 B. 3 C. 4 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
A. y=3(x+1)2+2 B. y=3(x+1)2﹣2
C. y=3(x﹣1)2+2 D. y=3(x﹣1)2﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣3x+7=0的两根为x1,x2,则下列表示正确的是( )
A. x1+x2=3,x1x2=7 B. x1+x2=﹣3,x1x2=7
C. x1+x2=﹣3,x1x2=﹣7 D. 以上全不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的内角和为1080°,则这个多边形的边数为 .
相关试题

