【题目】△OAB是以正多边形相邻的两个顶点A,B与它的中心O为顶点的三角形,若△OAB的一个内角为70°,则该正多边形的边数为.
参考答案:
【答案】9
【解析】当∠OAB=70°时,∠AOB=40°,则多边形的边数是:360÷40=9;当∠AOB=70°时,360÷70结果不是整数,故不符合条件.故答案是:9.
【考点精析】根据题目的已知条件,利用正多边形和圆的相关知识可以得到问题的答案,需要掌握圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x﹣3)2+|x﹣y+6|=0,则x+y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠BDC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化简计算
(1)(x﹣2y)(x+y);
(2)(x﹣1)(2x+1)﹣2(x﹣5)(x+2). -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 ; (2)
; (2) ;
;(3)
 ; (4)
; (4) ;
;(5)
 ; (6)
; (6) ;
; -
科目: 来源: 题型:
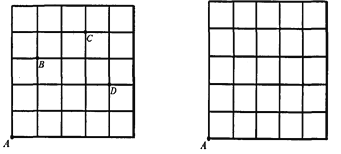
查看答案和解析>>【题目】在边长为1的小正方形组成的网格中,把一个点先沿水平方向平移|a|格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移|b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的点,我们把这个过程记为(a,b).
例如,从A到B记为:A→B(+l,+3);从C到D记为:C→D(+1,-2),
回答下列问题:
(1)如图1,若点A的运动路线为:A→B→C→A,请计算点A运动过的总路程.
(2)若点A运动的路线依次为:A→M(+2,+3),M→N(+1,-1),N→P(-2,+2),P→Q(+4,-4).请你依次在图2上标出点M、N、P、Q的位置.
(3)在图2中,若点A经过(m,n)得到点E,点E再经过(p,q)后得到Q,则m与p满足的数量关系是 ;n与q满足的数量关系是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.2x4﹣x2=x2
B.(2x2)4=8x8
C.x2x3=x6
D.(﹣x)6÷(﹣x)2=x4
相关试题

