【题目】定义:长宽比为![]() :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为![]() 矩形.
矩形.
下面,我们通过折叠的方式折出一个![]() 矩形,如图①所示.
矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为![]() 矩形.
矩形.
证明:设正方形ABCD的边长为1,则BD=![]() =
=![]() .
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.
∴EF∥AD.
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∴BF=![]() .
.
∴BC:BF=1:![]() =
=![]() :1.
:1.
∴四边形BCEF为![]() 矩形.
矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;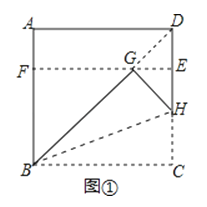
(2)已知四边形BCEF为![]() 矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是
矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是![]() 矩形;
矩形;
(3)将图②中的![]() 矩形BCMN沿用(2)中的方式操作3次后,得到一个“
矩形BCMN沿用(2)中的方式操作3次后,得到一个“![]() 矩形”,则n的值是 .
矩形”,则n的值是 .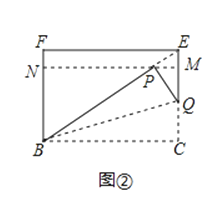
参考答案:
【答案】
(1)GH、DG;![]()
(2)
∵BC=1,EC=BF=![]() ,
,
∴BE=![]() =
=![]() .
.
由折叠可得BP=BC=1,∠FNM=∠BNM=90°,∠EMN=∠CMN=90°.
∵四边形BCEF是矩形,
∴∠F=∠FEC=∠C=∠FBC=90°,
∴四边形BCMN是矩形,∠BNM=∠F=90°,
∴MN∥EF,
∴![]() =
=![]() ,即BPBF=BEBN,
,即BPBF=BEBN,
∴1×![]() =
=![]() BN,
BN,
∴BN=![]() ,
,
∴BC:BN=1:![]() =
=![]() :1,
:1,
∴四边形BCMN是![]() 的矩形;
的矩形;
(3)6
【解析】(1)由折叠可得:
DG=HG,GH=CH,
∴DG=GH=CH.
设HC=x,则DG=GH=x.
∵∠DGH=90°,∴DH=![]() x,
x,
∴DC=DH+CH=![]() x+x=1,
x+x=1,
解得x=![]() .
.
∴tan∠HBC=![]() =
=![]() =
=![]() .
.
所以答案是:GH、DG,![]()
(3)同理可得:
将![]() 矩形沿用(2)中的方式操作1次后,得到一个“
矩形沿用(2)中的方式操作1次后,得到一个“![]() 矩形”,
矩形”,
将![]() 矩形沿用(2)中的方式操作1次后,得到一个“
矩形沿用(2)中的方式操作1次后,得到一个“![]() 矩形”,
矩形”,
将![]() 矩形沿用(2)中的方式操作1次后,得到一个“
矩形沿用(2)中的方式操作1次后,得到一个“![]() 矩形”,
矩形”,
所以将图②中的![]() 矩形BCMN沿用(2)中的方式操作3次后,得到一个“
矩形BCMN沿用(2)中的方式操作3次后,得到一个“![]() 矩形”,
矩形”,
所以答案是6.
【考点精析】根据题目的已知条件,利用勾股定理的概念和正方形的性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
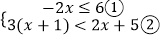 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的阶级在数轴上表示出来;
(Ⅳ)原不等式组的解集为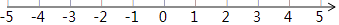
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一些体积为1
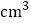 的小立方体恰好可以组成体积为1
的小立方体恰好可以组成体积为1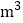 的大立方体,把所有这些小立方体一个接一个向上摞起来,大概有多高呢?以下选项中最接近这一高度的是( )
的大立方体,把所有这些小立方体一个接一个向上摞起来,大概有多高呢?以下选项中最接近这一高度的是( )A. 莲花山望海观音的高度 B. 滴水岩森林公园青萝嶂高度
C. 广州塔的高度 D. 国际航班飞行高度
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次初中生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
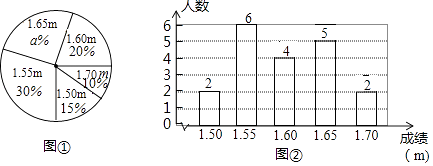
(1)①中a的值为;
(2)统计的这组初赛成绩数据的平均数、众数和中位数(结果保留小数点后两位);
(3)据这组初赛成绩,由高到低确定7人进入复赛,请直接写出初赛成绩为1.60m的运动员能否进入复赛. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.
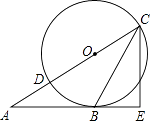
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:
 ,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,  取1.73.
取1.73.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
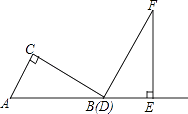
(1)当点C落在边EF上时,x=cm;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.
相关试题

