【题目】如图所示,某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1: ![]() ,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() 取1.73.
取1.73.
参考答案:
【答案】解:过点D作DM⊥BC于点M,DN⊥AC于点N,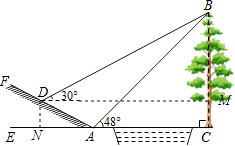
则四边形DMCN是矩形,
∵DA=6,斜坡FA的坡比i=1: ![]() ,
,
∴DN= ![]() AD=3,AN=ADcos30°=6×
AD=3,AN=ADcos30°=6× ![]() =3
=3 ![]() ,
,
设大树的高度为x,
∵在斜坡上A处测得大树顶端B的仰角是48°,
∴tan48°= ![]() ≈1.11,
≈1.11,
∴AC= ![]() ,
,
∴DM=CN=AN+AC=3 ![]() +
+ ![]() ,
,
∵在△ADM中, ![]() =
= ![]() ,
,
∴x﹣3=(3 ![]() +
+ ![]() )
) ![]() ,
,
解得:x≈13.
答:树高BC约13米
【解析】首先过点D作DM⊥BC于点M,DN⊥AC于点N,由FA的坡比i=1: ![]() ,DA=6,可求得AN与DN的长,然后设大树的高度为x,又由在斜坡上A处测得大树顶端B的仰角是48°,可得AC=
,DA=6,可求得AN与DN的长,然后设大树的高度为x,又由在斜坡上A处测得大树顶端B的仰角是48°,可得AC= ![]() ,又由在△ADM中,
,又由在△ADM中, ![]() =
= ![]() ,可得x﹣3=(3
,可得x﹣3=(3 ![]() +
+ ![]() )
) ![]() ,继而求得答案.
,继而求得答案.
【考点精析】认真审题,首先需要了解关于仰角俯角问题(仰角:视线在水平线上方的角;俯角:视线在水平线下方的角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次初中生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
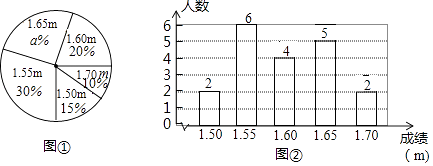
(1)①中a的值为;
(2)统计的这组初赛成绩数据的平均数、众数和中位数(结果保留小数点后两位);
(3)据这组初赛成绩,由高到低确定7人进入复赛,请直接写出初赛成绩为1.60m的运动员能否进入复赛. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:长宽比为
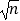 :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为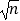 矩形.
矩形.
下面,我们通过折叠的方式折出一个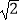 矩形,如图①所示.
矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为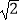 矩形.
矩形.
证明:设正方形ABCD的边长为1,则BD=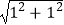 =
=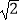 .
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.
∴EF∥AD.
∴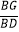 =
=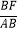 ,即
,即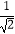 =
=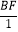 .
.
∴BF=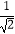 .
.
∴BC:BF=1: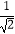 =
=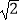 :1.
:1.
∴四边形BCEF为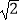 矩形.
矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;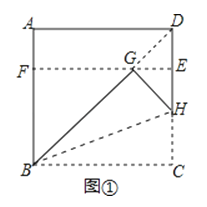
(2)已知四边形BCEF为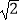 矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是
矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是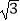 矩形;
矩形;
(3)将图②中的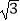 矩形BCMN沿用(2)中的方式操作3次后,得到一个“
矩形BCMN沿用(2)中的方式操作3次后,得到一个“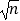 矩形”,则n的值是 .
矩形”,则n的值是 .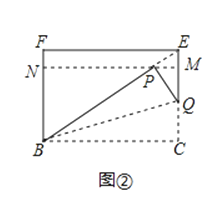
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.
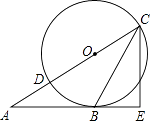
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
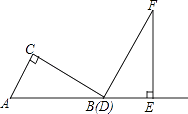
(1)当点C落在边EF上时,x=cm;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.

(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;
(3)在图②中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
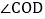 在
在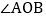 的内部,OM平分
的内部,OM平分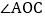 ,ON平分
,ON平分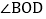
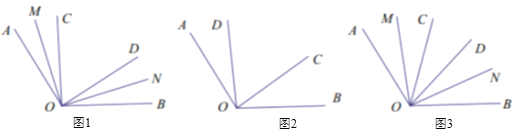
(1)如图1,
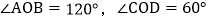 时,当OC在OD的左侧,求
时,当OC在OD的左侧,求 的度数.
的度数.(2)如图2,
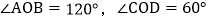 时,当OC在OD的右侧 ,请补全图形,并求
时,当OC在OD的右侧 ,请补全图形,并求 的度数.
的度数.(3)如图3,当
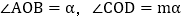 ,且OC在OD左侧时,试用
,且OC在OD左侧时,试用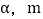 的代数式表示
的代数式表示 .
.
相关试题

