【题目】解不等式组 ![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的阶级在数轴上表示出来;
(Ⅳ)原不等式组的解集为![]()
参考答案:
【答案】x≥﹣3;x<2;![]() ;﹣3≤x<2
;﹣3≤x<2
【解析】解:(Ⅰ)系数化成1得x≥﹣3. 故答案是:x≥﹣3;
(Ⅱ)去括号,得3x+3<2x+5,
移项,得3x﹣2x<5﹣3,
合并同类项,得x<2.
故答案是:x<2;
(Ⅳ)不等式组的解集是﹣3≤x<2.
故答案是:﹣3≤x<2.
【考点精析】通过灵活运用不等式的解集在数轴上的表示和一元一次不等式组的解法,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为
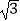 ,则HD的长为 .
,则HD的长为 . 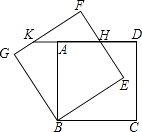
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:所谓完全平方式,就是对于一个整式A,如果存在另一个整式B,使得A=B2 , 则称A是完全平方式,例如a4=(a2)2 , 4a2﹣4a+1=(2a﹣1)2 .
(1)下列各式中完全平方式的编号有________;
①a6;②a2+ab+b2;③x2﹣4x+4y2④m2+6m+9;⑤x2﹣10x﹣25;⑥4a2+2ab+
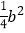 .
. (2)若4x2+xy+my2和x2﹣nxy+64y2都是完全平方式,求m2015n2016的值;
(3)多项式49x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是哪些?(请罗列出所有可能的情况,直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一些体积为1
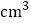 的小立方体恰好可以组成体积为1
的小立方体恰好可以组成体积为1 的大立方体,把所有这些小立方体一个接一个向上摞起来,大概有多高呢?以下选项中最接近这一高度的是( )
的大立方体,把所有这些小立方体一个接一个向上摞起来,大概有多高呢?以下选项中最接近这一高度的是( )A. 莲花山望海观音的高度 B. 滴水岩森林公园青萝嶂高度
C. 广州塔的高度 D. 国际航班飞行高度
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次初中生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
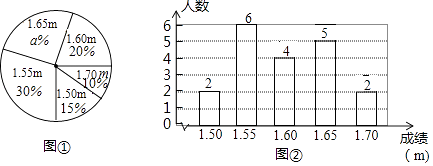
(1)①中a的值为;
(2)统计的这组初赛成绩数据的平均数、众数和中位数(结果保留小数点后两位);
(3)据这组初赛成绩,由高到低确定7人进入复赛,请直接写出初赛成绩为1.60m的运动员能否进入复赛. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:长宽比为
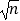 :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为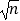 矩形.
矩形.
下面,我们通过折叠的方式折出一个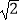 矩形,如图①所示.
矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为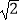 矩形.
矩形.
证明:设正方形ABCD的边长为1,则BD=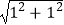 =
=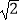 .
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.
∴EF∥AD.
∴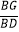 =
=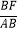 ,即
,即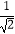 =
=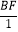 .
.
∴BF=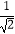 .
.
∴BC:BF=1: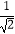 =
=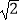 :1.
:1.
∴四边形BCEF为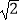 矩形.
矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;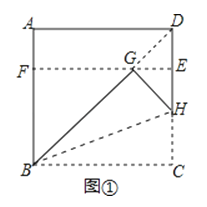
(2)已知四边形BCEF为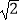 矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是
矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是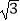 矩形;
矩形;
(3)将图②中的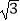 矩形BCMN沿用(2)中的方式操作3次后,得到一个“
矩形BCMN沿用(2)中的方式操作3次后,得到一个“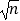 矩形”,则n的值是 .
矩形”,则n的值是 .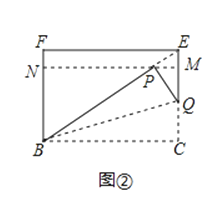
相关试题

