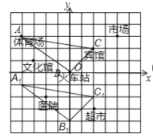
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:

(1)请你以火车站为原点建立平面直角坐标系,若以小方格的边长为单位长度,写出市场的坐标为_______;超市的坐标为_____________.
(2)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将△ABC向下平移4个单位长度,画出平移后的![]() ,写出
,写出![]() 的坐标.
的坐标.
(3)求出![]() 的面积.
的面积.
参考答案:
【答案】(1)建立坐标系见解析;(4,3);(2,-3);(2)图见解析;![]() ;(3)7
;(3)7
【解析】
(1)以火车站为原点建立平面直角坐标系,然后根据平面直角坐标系即可写出结论;
(2)顺次连接体育场A、宾馆C和火车站B,可得△ABC,然后将△ABC向下平移4个单位长度,得到![]() 即可,然后根据平面直角坐标系即可写出各点坐标即可;
即可,然后根据平面直角坐标系即可写出各点坐标即可;
(3)利用长方形的面积减去3个直角三角形的面积即可求出结论.
解:(1)以火车站为原点建立平面直角坐标系,如下图所示,由平面直角坐标系可知:市场的坐标为(4,3),超市的坐标为(2,-3)
故答案为:(4,3);(2,-3);
(2)顺次连接体育场A、宾馆C和火车站B,可得△ABC,然后将△ABC向下平移4个单位长度,得到![]() ,如下图所示,
,如下图所示,![]() 即为所求,由平面直角坐标系可知:
即为所求,由平面直角坐标系可知:![]() ;
;
(3)由坐标系可得:![]() =6×3-
=6×3-![]() ×6×1-
×6×1-![]() ×4×3-
×4×3-![]() ×2×2=7
×2×2=7
-
科目: 来源: 题型:
查看答案和解析>>【题目】取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图1,先把正方形ABCD对折,折痕为MN.
第二步:点G在线段 MD上,将△GCD沿GC翻折,点D恰好落在MN上,记为点P,连接BP.
(1)判断△PBC的形状,并说明理由;
(2)作点C关于直线AP的对称点C′,连接PC′、DC′.
①在图2中补全图形,并求出∠APC′的度数;
②猜想∠PC′D的度数,并加以证明;(温馨提示:当你遇到困难时,不妨连接AC′、CC′,研究图形中特殊的三角形)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,O为数轴的原点,A,B分别为数轴上的两点,A点对应的数为﹣30,B点对应的数为100.
(1)A、B的中点C对应的数是 ;
(2)若点D数轴上A、B之间的点,D到B的距离是D到A的距离的3倍,求D对应的数.(提示:数轴上右边的点对应的数减去左边对应的数等于这两点间的距离);
(3)若P点和Q点是数轴上的两个动点,当P点从B点出发,以6个单位长度/秒的速度向左运动时,Q点也从A点出发,以4个单位长度/秒的速度向右运动,设两点在数轴上的E点处相遇,那么E点对应的数是多少?

-
科目: 来源: 题型:
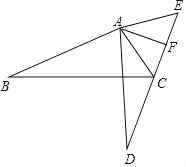
查看答案和解析>>【题目】如图,∠BAD=∠CAE,AB=AD,AC=AE.且E,F,C,D在同一直线上.
(1)求证:△ABC≌△ADE;
(2)若∠B=30°,∠BAC=100°,点F是CE的中点,连结AF,求∠FAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店分两次购进
 、
、 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:购进数量(件)
购进所需费用(元)
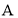
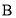
第一次
30
40
3800
第二次
40
30
3200
(1)求
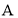 、
、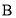 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?(2)商场决定
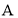 种商品以每件30元出售,
种商品以每件30元出售,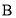 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进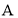 、
、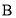 两种商品共1000件,且
两种商品共1000件,且 种商品的数量不少于
种商品的数量不少于 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.
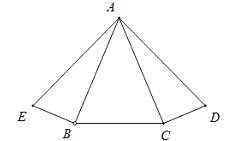
请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( )
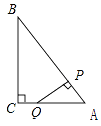
A.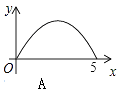
B.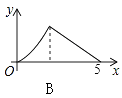
C.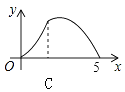
D.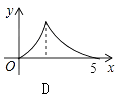
相关试题

