【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为边在
为边在![]() 轴上方作正方形
轴上方作正方形![]() ,点
,点![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线与
的垂线与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的函数关系表达式;
(2)当点![]() 在线段
在线段![]() (点
(点![]() 不与
不与![]() 重合)上运动至何处时,线段
重合)上运动至何处时,线段![]() 的长有最大值?并求出这个最大值;
的长有最大值?并求出这个最大值;
(3)在第四象限的抛物线上任取一点![]() ,连接
,连接![]() .请问:
.请问:![]() 的面积是否存在最大值?若存在,求出此时点
的面积是否存在最大值?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
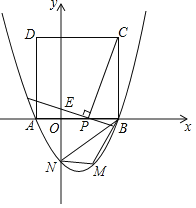
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 时,线段
时,线段![]() 有最大值.最大值是
有最大值.最大值是![]() ;(3)
;(3)![]() 时,
时,![]() 的面积有最大值,最大值是
的面积有最大值,最大值是![]() ,此时
,此时![]() 点的坐标为
点的坐标为![]() .
.
【解析】
(1)将点![]() 的坐标代入二次函数表达式,即可求解;
的坐标代入二次函数表达式,即可求解;
(2)设![]() ,则
,则![]() ,由
,由![]() 得出比例线段,可表示
得出比例线段,可表示![]() 的长,利用二次函数的性质可求出线段
的长,利用二次函数的性质可求出线段![]() 的最大值;
的最大值;
(3)过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,由
,由![]() 即可求解.
即可求解.
解:(1))∵抛物线![]() 经过
经过![]() ,
,![]() ,
,
把![]() 两点坐标代入上式,
两点坐标代入上式,![]() ,
,
解得:![]() ,
,
故抛物线函数关系表达式为![]() ;
;
(2)∵![]() ,点
,点![]() ,
,
∴![]() ,
,
∵正方形![]() 中,
中,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 时,线段
时,线段![]() 长有最大值,最大值为
长有最大值,最大值为![]() .
.
即![]() 时,线段
时,线段![]() 有最大值.最大值是
有最大值.最大值是![]() .
.
(3)存在.
如图,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,
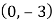
∵抛物线的解析式为![]() ,
,
∴![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 时,
时,![]() 的面积有最大值,最大值是
的面积有最大值,最大值是![]() ,此时
,此时![]() 点的坐标为
点的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
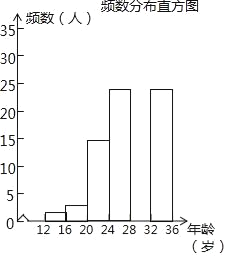
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.骑共享单车的人数统计表
年龄段(岁)
频数
频率
12≤x<16
2
0.02
16≤x<20
3
0.03
20≤x<24
15
a
24≤x<28
25
0.25
28≤x<32
b
0.30
32≤x<36
25
0.25
根据以上信息解答下列问题:
①统计表中的a= ;b= ;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进
 、
、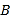 两种商品,购买1个
两种商品,购买1个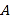 商品比购买1个
商品比购买1个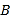 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买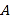 商品和花费100元购买
商品和花费100元购买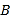 商品的数量相等.
商品的数量相等.(1)求购买一个
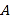 商品和一个
商品和一个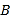 商品各需要多少元;
商品各需要多少元;(2)商店准备购买
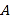 、
、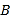 两种商品共80个,若
两种商品共80个,若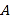 商品的数量不少于
商品的数量不少于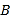 商品数量的4倍,并且购买
商品数量的4倍,并且购买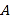 、
、 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案? -
科目: 来源: 题型:
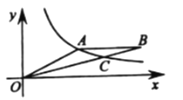
查看答案和解析>>【题目】如图,
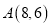 是反比例函数
是反比例函数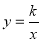 在第一象限图像上一点,连接
在第一象限图像上一点,连接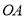 ,过
,过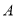 作
作 轴,截取
轴,截取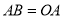 (
( 在
在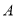 右侧),连接
右侧),连接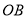 ,交反比例函数
,交反比例函数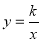 的图像于点
的图像于点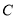 .
.
(1)求反比例函数
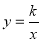 的表达式;
的表达式;(2)求点
 的坐标及
的坐标及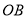 所在直线解析式;
所在直线解析式;(3)求
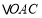 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面内有一点
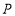 到
到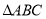 的三个顶点的距离分别为
的三个顶点的距离分别为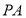 、
、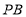 、
、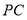 ,若有
,若有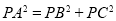 ,则称点
,则称点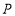 为
为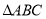 关于点
关于点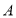 的勾股点.
的勾股点.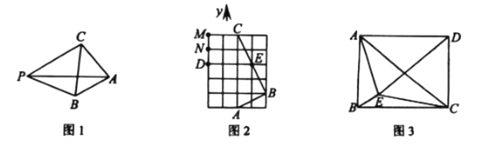
(1)如图2,在
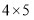 的网格中,每个小正方形的边长均为1,点
的网格中,每个小正方形的边长均为1,点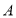 、
、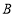 、
、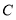 、
、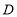 、
、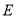 、
、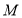 、
、 均在小正方形的顶点上,则点E是
均在小正方形的顶点上,则点E是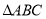 关于点B的勾股点.
关于点B的勾股点.(2)如图3,
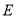 是矩形
是矩形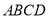 内一点,且点
内一点,且点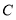 是
是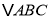 关于点
关于点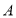 的勾股点,
的勾股点,①求证:
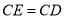 ;
;②若
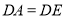 ,
, ,求
,求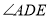 的度数.
的度数.(3)如图3,矩形
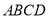 中,
中, ,
,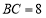 ,
,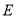 是矩形
是矩形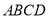 内一点,且点
内一点,且点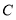 是
是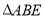 关于点
关于点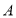 的勾股点.
的勾股点.①当
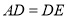 时,求
时,求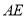 的长;
的长;②直接写出
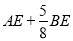 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙,无重叠的四边形EFGH,设AB=a,BC=b,若AH=1,则( )
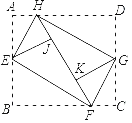
A.a2=4b﹣4B.a2=4b+4C.a=2b﹣1D.a=2b+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2
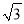 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).
米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).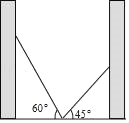
相关试题

