【题目】如图1,平面内有一点![]() 到
到![]() 的三个顶点的距离分别为
的三个顶点的距离分别为![]() 、
、![]() 、
、![]() ,若有
,若有![]() ,则称点
,则称点![]() 为
为![]() 关于点
关于点![]() 的勾股点.
的勾股点.
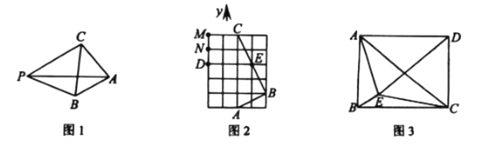
(1)如图2,在![]() 的网格中,每个小正方形的边长均为1,点
的网格中,每个小正方形的边长均为1,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均在小正方形的顶点上,则点E是
均在小正方形的顶点上,则点E是![]() 关于点B的勾股点.
关于点B的勾股点.
(2)如图3,![]() 是矩形
是矩形![]() 内一点,且点
内一点,且点![]() 是
是![]() 关于点
关于点![]() 的勾股点,
的勾股点,
①求证:![]() ;
;
②若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(3)如图3,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是矩形
是矩形![]() 内一点,且点
内一点,且点![]() 是
是![]() 关于点
关于点![]() 的勾股点.
的勾股点.
①当![]() 时,求
时,求![]() 的长;
的长;
②直接写出![]() 的最小值.
的最小值.
参考答案:
【答案】(2)①证明见解析;②30°;(3)①AE的长为![]() 或
或![]() ;②
;②![]() .
.
【解析】
(2)①由矩形性质得∠ADC=90°,可得AD2+DC2=AC2;根据勾股数得BC2+EC2=AC2,又因为AD=BC,即得CE=CD.
②设∠CED=α,根据∠AEC=135°和CE=CD即∠ADC=90°,可用α表示△ADE的三个内角,利用三角形内角和180°为等量关系列方程,即求出α进而求出∠ADE.
(3)由条件“点C是△ABE关于点A的勾股点”仍可得CE=CD=5,作为条件使用.①△ADE是等腰三角形需分3种情况讨论,把每种情况画图再根据矩形性质和勾股定理计算,即能求AE的长.②在CB上截取CH=![]() ,利用两边对应成比例及夹角相等构造△ECH∽△BCE,把
,利用两边对应成比例及夹角相等构造△ECH∽△BCE,把![]() BE转化为EH,所以当点A、E、H在同一直线上时,AE+
BE转化为EH,所以当点A、E、H在同一直线上时,AE+![]() BE=AH取得最小值,利用勾股定理求出AH即可.
BE=AH取得最小值,利用勾股定理求出AH即可.
解:(2)①证明:∵点C是△ABE关于点A的勾股点
∴CA2=CB2+CE2
∵四边形ABCD是矩形
∴AB=CD,AD=BC,∠ADC=90°
∴CA2=AD2+CD2=CB2+CD2
∴CB2+CE2=CB2+CD2
∴CE=CD
②设∠CED=α,则∠CDE=∠CED=α
∴∠ADE=∠ADC-∠CDE=90°-α
∵∠AEC=135°
∴∠AED=∠AEC-∠CED=135°-α
∵DA=DE
∴∠DAE=∠DEA=135°-α
∵∠DAE+∠DEA+∠ADE=180°
∴2(135°-α)+(90°-α)=180°
解得:α=60°
∴∠ADE=90°-60°=30°
(3)①∵矩形ABCD中,AB=5,BC=8
∴AD=BC=8,CD=AB=5
∵点C是△ABE关于点A的勾股点
∴CE=CD=5
i)如图1,若DE=DA,则DE=8
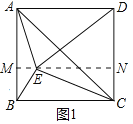
过点E作MN⊥AB于点M,交DC于点N
∴∠AME=∠MND=90°
∴四边形AMND是矩形
∴MN=AD=8,AM=DN
设AM=DN=x,则CN=CD-DN=5-x
∵Rt△DEN中,EN2+DN2=DE2;Rt△CEN中,EN2+CN2=CE2
∴DE2-DN2=CE2-CN2
∴82-x2=52-(5-x)2
解得:x=![]()
∴EN=![]() ,AM=DN=
,AM=DN=![]()
∴ME=MN-EN=8-![]() ,
,
∴Rt△AME中,AE=![]()
ii)如图2,若AE=DE,则E在AD的垂直平分线上
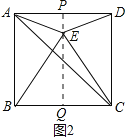
过点E作PQ⊥AD于点P,交BC于点Q
∴AP=DP=![]() AD=4,∠APQ=∠PQC=90°
AD=4,∠APQ=∠PQC=90°
∴四边形CDPQ是矩形
∴PQ=CD=5,CQ=PD=4
∴Rt△CQE中,EQ=![]() =3
=3
∴PE=PQ-EQ=2
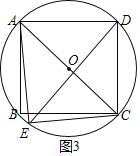
∴Rt△APE中,AE=![]()
iii)如图3,若AE=AD=8,则AE2+CE2=AD2+CD2=AC2
∴∠AEC=90°
取AC中点O,则点A、B、C、D在以O为圆心、OA为半径的⊙O上
∴点E也在⊙O上
∴点E不在矩形ABCD内部,不符合题意
综上所述,若△ADE是等腰三角形,AE的长为![]() 或
或![]() .
.
②在CB上截取CH=![]() ,连接EH
,连接EH
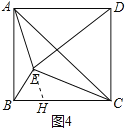
∴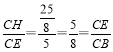 ,
,
∵∠ECH=∠BCE
∴△ECH∽△BCE
∴![]() ,
,
∴EH=![]() BE
BE
∴AE+![]() BE=AE+EH
BE=AE+EH
∴当点A、E、H在同一直线上时,AE+![]() BE=AH取得最小值
BE=AH取得最小值
∵BH=BC-CH=8-![]() =
=![]() ,
,
∴AH=![]()
∴AE+![]() BE的最小值为
BE的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进
 、
、 两种商品,购买1个
两种商品,购买1个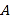 商品比购买1个
商品比购买1个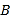 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买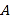 商品和花费100元购买
商品和花费100元购买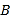 商品的数量相等.
商品的数量相等.(1)求购买一个
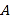 商品和一个
商品和一个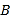 商品各需要多少元;
商品各需要多少元;(2)商店准备购买
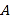 、
、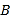 两种商品共80个,若
两种商品共80个,若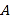 商品的数量不少于
商品的数量不少于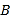 商品数量的4倍,并且购买
商品数量的4倍,并且购买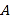 、
、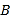 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案? -
科目: 来源: 题型:
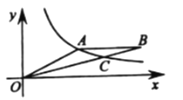
查看答案和解析>>【题目】如图,
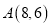 是反比例函数
是反比例函数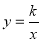 在第一象限图像上一点,连接
在第一象限图像上一点,连接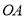 ,过
,过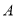 作
作 轴,截取
轴,截取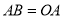 (
( 在
在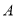 右侧),连接
右侧),连接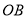 ,交反比例函数
,交反比例函数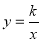 的图像于点
的图像于点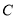 .
.
(1)求反比例函数
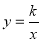 的表达式;
的表达式;(2)求点
 的坐标及
的坐标及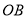 所在直线解析式;
所在直线解析式;(3)求
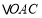 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
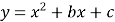 的图象与
的图象与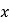 轴交于点
轴交于点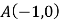 和点
和点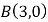 ,与
,与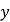 轴交于点
轴交于点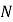 ,以
,以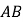 为边在
为边在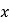 轴上方作正方形
轴上方作正方形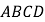 ,点
,点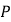 是
是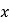 轴上一动点,连接
轴上一动点,连接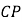 ,过点
,过点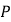 作
作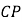 的垂线与
的垂线与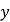 轴交于点
轴交于点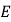 .
.(1)求该抛物线的函数关系表达式;
(2)当点
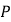 在线段
在线段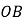 (点
(点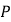 不与
不与 重合)上运动至何处时,线段
重合)上运动至何处时,线段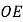 的长有最大值?并求出这个最大值;
的长有最大值?并求出这个最大值;(3)在第四象限的抛物线上任取一点
 ,连接
,连接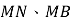 .请问:
.请问: 的面积是否存在最大值?若存在,求出此时点
的面积是否存在最大值?若存在,求出此时点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.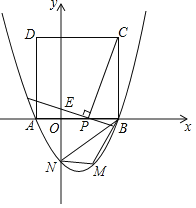
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙,无重叠的四边形EFGH,设AB=a,BC=b,若AH=1,则( )
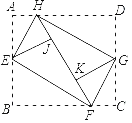
A.a2=4b﹣4B.a2=4b+4C.a=2b﹣1D.a=2b+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2
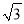 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).
米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).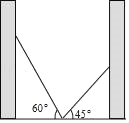
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
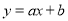 ,反比例函数
,反比例函数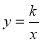 (a,b,k是常数,且
(a,b,k是常数,且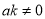 ),若其中一部分x,y的对应值如表:则不等式
),若其中一部分x,y的对应值如表:则不等式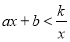 的解集是_________.
的解集是_________.x

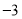
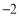
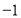
1
2
3
4
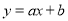
3
2
1
0
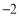
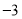

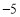
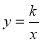
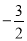
2
3
6
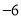
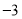
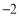
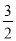
相关试题

