【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=3,b=4,c=5; ②a=6,∠A=45°;③a=2,b=2,c=2![]() ; ④∠A=38°,∠B=52°.
; ④∠A=38°,∠B=52°.
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】①a=3,b=4,c=5,
∵32+42=25=52,
∴满足①的三角形为直角三角形;
②a=6,∠A=45°,
只此两个条件不能断定三角形为直角三角形;
③a=2,b=2, ![]() ,
,
∵22+22=8=![]() ,
,
∴满足③的三角形为直角三角形;
④∵∠A=38°,∠B=52°,
∴∠C=180°∠A∠B=90°,
∴满足④的三角形为直角三角形。
综上可知:满足①③④的三角形均为直角三角形。
故选C.
点睛:根据勾股定理的逆定理以及直角三角形的定义,验证四组条件中数据是否满足“较小两边平方的和等于最大边的平方”或“有一个角是直角”,由此即可得出结论.
-
科目: 来源: 题型:
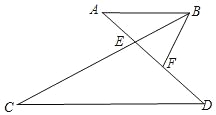
查看答案和解析>>【题目】如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
(1)求证:FB2=FEFA;
(2)若BF=3,EF=2,求△ABE与△BEF的面积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①b2>4ac ②2a+b=0 ③c﹣a<0 ④若点B(﹣4,y1)、C(1,y2)为函数图象上的两点,则y1<y2,其中正确结论是( )
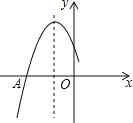
A.②④ B.②③ C.①③ D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,表示小王骑自行车和小李骑摩托车者沿相同的路线由甲地到乙地行驶过程的函数图象,两地相距80千米,请根据图象解决下列问题:
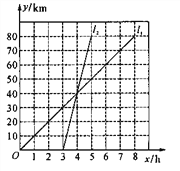
⑴
 是 车行驶过程的函数图象,
是 车行驶过程的函数图象,  是 车行驶过程的函数图象.
是 车行驶过程的函数图象.⑵哪一个人出发早?早多长时间?哪一个人早到达目的地?早多长时间?
⑶求出两个人在途中行驶的速度是多少?
⑷分别求出表示自行车和摩托车行驶过程的函数解析式,并求出自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=
 ∠EOC,∠DOE=70°,求∠EOC的度数.
∠EOC,∠DOE=70°,求∠EOC的度数. 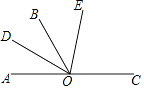
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】从多边形的一个顶点出发引对角线,可以把这个多边形分割成7个三角形,则该多边形为 边形。
相关试题

