Question

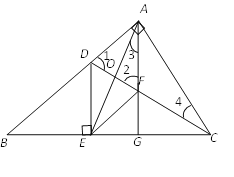
【题目】如图9.1，在△ABC中，∠BAC=90°，点D为AB边上的一点，过点D作DE⊥BC于E，连接CD，过点A作AF∥DE交CD于点F，交BC于点G，连接EF.

（1）求证：△BED∽△BAC；

（2）写出所有与△BED相似的三角形（△BAC除外）；

（3）如图9.2，若四边形ADEF是菱形，连接对角线AE与DF相交于点O.

①求证：OA2=OC·OF；

②当AE=12，CF=5时，求OF的长，并直接写出△BED与△BAC的相似比的值.

Answer 1

【答案】（1）证明见解析；（2）△BED∽△BGA ，△BED∽△AGC；（3）①证明见解析；②.

【解析】试题分析：（1）根据两角对应相等两三角形相似即可判定．

（2）根据相似三角形的判定方法即可判断．

（3）①只要证明△OAF∽△OCA，可得，由此即可证明．

②利用勾股定理求出DE、AC即可解决问题．

试题解析：（1）∵DE⊥BC，∠BAC=90°

∴ ∠BED=∠BAC=90°，

∵ ∠B=∠B.

∴ △BED∽△BAC

（2）△BED∽△BGA ，△BED∽△AGC

（3）①如图，∵四边形ADEF是菱形，

∴AD=AF，AE⊥DF

∴ ∠1=∠2，∠AOF=90°

∴ ∠2+∠3=90°.

∵∠BAC=90°，

∴ ∠1+∠4=90°.

∴ ∠3=∠4.

∵∠AOC=∠AOC.

∴ △OAF∽△OCA.

∴,

∴OA2=OC·OF.

②设OF=x，则OC=x+5.

∵四边形ADEF是菱形，AE=12，

∴OA=AE=6

由①可知OA2=OC·OF，列方程得：36=x(x+5)，

解得：x1=4，x2=-9（不合题意，舍去）

∴OF的长为4.

△BED与△BAC的相似比.