【题目】如图,已知![]() 是三角形纸片
是三角形纸片![]() 的高,将纸片沿直线
的高,将纸片沿直线![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,给出下列判断:
重合,给出下列判断:

①![]() 是
是![]() 的中位线;
的中位线;
②![]() 的周长等于
的周长等于![]() 周长的一半:
周长的一半:
③若四边形![]() 是菱形,则
是菱形,则![]() ;
;
④若![]() 是直角,则四边形
是直角,则四边形![]() 是矩形.
是矩形.
其中正确的是( )
A.①②③B.①②④C.②④D.①③④
参考答案:
【答案】A
【解析】
根据折叠可得EF是AD的垂直平分线,再加上条件AD是三角形纸片ABC的高可以证明EF∥BC,进而可得△AEF∽△ABC,从而得![]() ,进而得到EF是△ABC的中位线;再根据三角形的中位线定理可判断出△AEF的周长是△ABC的一半,进而得到△DEF的周长等于△ABC周长的一半;根据三角形中位线定理可得AE=
,进而得到EF是△ABC的中位线;再根据三角形的中位线定理可判断出△AEF的周长是△ABC的一半,进而得到△DEF的周长等于△ABC周长的一半;根据三角形中位线定理可得AE=![]() AB,AF=
AB,AF=![]() AC,若四边形AEDF是菱形则AE=AF,即可得到AB=AC.
AC,若四边形AEDF是菱形则AE=AF,即可得到AB=AC.

解:∵AD是△ABC的高,
∴AD⊥BC,
∴∠ADC=90°,
根据折叠可得:EF是AD的垂直平分线,
∴AO=DO=![]() AD,AD⊥EF,
AD,AD⊥EF,
∴∠AOF=90°,
∴∠AOF=∠ADC=90°,
∴EF∥BC,
∴△AEF∽△ABC,
![]() ,
,
∴EF是△ABC的中位线,
故①正确;
∵EF是△ABC的中位线,
∴△AEF的周长是△ABC的一半,
根据折叠可得△AEF≌△DEF,
∴△DEF的周长等于△ABC周长的一半,
故②正确;
∵EF是△ABC的中位线,
∴AE=![]() AB,AF=
AB,AF=![]() AC,
AC,
若四边形AEDF是菱形,
则AE=AF,
∴AB=AC,
故③正确;
根据折叠只能证明∠BAC=∠EDF=90°,
不能确定∠AED和∠AFD的度数,故④错误;
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角尺按图①所示的方式叠放在一起,现将含45°角的三角尺ADE固定不动,把含30°角的三角尺ABC绕顶点A顺时针旋转角α(α=∠BAD且0°<α<180°),使两块三角尺至少有一组边平行.


(1)如图②,当α=________°时,BC∥DE.
(2)请你分别在图③,④中,各画一种符合要求的图形,标出α,并完成下列各题.
图③中,当α=________°时,________∥________;
图④中,当α=________°时,________∥________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为直线x=
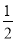 的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5(1)求A、B两点的坐标及该抛物线对应的解析式;
(2)D为BC的中点,延长OD与抛物线在第四象限内交于点E,连结AE、BE.
①求点E的坐标;
②判断ABE的形状,并说明理由;
(3)在x轴下方的抛物线上,是否存在一点P,使得四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为
 ,C点的坐标为
,C点的坐标为 ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着 的路线移动
的路线移动 即:沿着长方形移动一周
即:沿着长方形移动一周 .
. 写出点B的坐标
写出点B的坐标 ______
______
 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标. 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
相关试题

