搜索
【题目】如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为
，C点的坐标为
，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着
的路线移动
即：沿着长方形移动一周
．
写出点B的坐标______
当点P移动了4秒时，描出此时P点的位置，并求出点P的坐标．
在移动过程中，当点P到x轴距离为5个单位长度时，求点P移动的时间．
参考答案：
【答案】（1）（4，6）（2）（2,6）（3）点P移动的时间2.5秒或5.5秒
【解析】
(1)根据长方形的性质易得点B的坐标.
(2)根据题意，点P的运动速度为每秒2个单位长度，当点P移动了4秒时，其运动了8个单位长度，此时点P的坐标为(4，4)，位于AB上.
(3)根据题意，当点P到x轴的距离为5个单位长度时，有两种情况，分情况讨论计算即可.
解：(1)根据长方形的性质，可得AB与y轴平行，BC与x轴平行，故点B的坐标为(4，6)．
(2)根据题意，点P的运动速度为每秒2个单位长度，当点P移动了4秒时，其运动了8个单位长度，此时点P的坐标为(4，4)，位于AB上，描点如图．
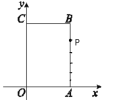
(3)根据题意，当点P到x轴的距离为5个单位长度时，有两种情况：当点P在AB上时，点P运动了4＋5＝9(个)单位长度，此时点P运动了4.5秒；当点P在OC上时，点P运动了4＋6＋4＋1＝15(个)单位长度，此时点P运动了7.5秒．
综上所述，点P移动了4.5秒或7.5秒．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2016次运动后，动点P的坐标是（ ）
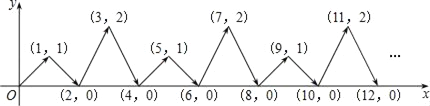
A. （2016，1） B. （2016，0） C. （2016，2） D. （2017，0）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正三角形和正方形的面积分别为10，6，两阴影部分的面积分别为a，b（a＞b），则（a﹣b）等于 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，E为AB边上一点，过点D作DF⊥DE，与BC延长线交于点F．连接EF，与CD边交于点G，与对角线BD交于点H．
（1）若BF=BD=
，求BE的长；（2）若∠ADE=2∠BFE，求证：FH=HE+HD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角梯形ABCD中，AD∥BC，∠B=90°，且AD=12cm，AB=8cm，DC=10cm，若动点P从A点出发，以每秒2cm的速度沿线段AD向点D运动；动点Q从C点出发以每秒3cm的速度沿CB向B点运动，当P点到达D点时，动点P、Q同时停止运动，设点P、Q同时出发，并运动了t秒，回答下列问题：
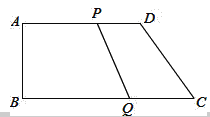
（1）BC= cm；
（2）当t为多少时，四边形PQCD成为平行四边形？
（3）当t为多少时，四边形PQCD为等腰梯形？
（4）是否存在t，使得△DQC是等腰三角形？若存在，请求出t的值；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D．
试说明：AC∥DF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知△ABC，求证：∠A+∠B+∠C=180°．
通过画平行线，将∠A、∠B、∠C作等角代换，使各角之和恰为一平角，依辅助线不同而得多种证法．
证法1：如图1，延长BC到D，过C画CE∥BA．
∵BA∥CE（作图2所知），
∴∠B=∠1，∠A=∠2（两直线平行，同位角、内错角相等）．
又∵∠BCD=∠BCA+∠2+∠1=180°（平角的定义），
∴∠A+∠B+∠ACB=180°（等量代换）．
如图3，过BC上任一点F，画FH∥AC，FG∥AB，这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗？请你试一试．
相关试题
