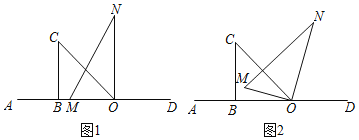
【题目】将一副直角三角板按如图1摆放在直线AD上![]() 直角三角板OBC和直角三角板MON,
直角三角板OBC和直角三角板MON,![]() ,
,![]() ,
,![]() ,
,![]() ,保持三角板OBC不动,将三角板MON绕点O以每秒
,保持三角板OBC不动,将三角板MON绕点O以每秒![]() 的速度顺时针方向旋转t秒
的速度顺时针方向旋转t秒![]()
![]() 如图2,
如图2,![]() ______度
______度![]() 用含t的式子表示
用含t的式子表示![]() ;
;
![]() 在旋转的过程中,是否存在t的值,使
在旋转的过程中,是否存在t的值,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒
直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒![]() 的速度顺时针旋转.
的速度顺时针旋转.
![]() 当
当![]() ______秒时,
______秒时,![]() ;
;
![]() 请直接写出在旋转过程中,
请直接写出在旋转过程中,![]() 与
与![]() 的数量关系
的数量关系![]() 关系式中不能含
关系式中不能含![]() .
.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)①5或10,②3∠NOD+4∠BOM=270°.
(3)①5或10,②3∠NOD+4∠BOM=270°.
【解析】
(1)把旋转前∠NOD的大小减去旋转的度数就是旋转后的∠NOD的大小.
(2)相对MO与CO的位置有两种情况,所以要分类讨论,然后根据∠NOD=4∠COM建立关于t的方程即可.
(3)①其实是一个追赶问题,分MO没有追上CO与MO超过CO两种情况,然后分别列方程即可.
②分别用t的代数式表示∠NOD和∠BOM,然后消去t即可得出它们的关系.
(1)∠NOD一开始为90°,然后每秒减少8°,因此∠NOD=90﹣8t.
故答案为:90﹣8t.
(2)当MO在∠BOC内部时,即t![]() 时,根据题意得:
时,根据题意得:
90﹣8t=4(45﹣8t)
解得:t![]() ;
;
当MO在∠BOC外部时,即t![]() 时,根据题意得:
时,根据题意得:
90﹣8t=4(8t﹣45)
解得:t![]() .
.
综上所述:t![]() 或t
或t![]() .
.
(3)①当MO在∠BOC内部时,即t![]() 时,根据题意得:
时,根据题意得:
8t﹣2t=30
解得:t=5;
当MO在∠BOC外部时,即t![]() 时,根据题意得:
时,根据题意得:
8t﹣2t=60
解得:t=10.
故答案为:5或10.
②∵∠NOD=90﹣8t,∠BOM=6t,∴3∠NOD+4∠BOM=3(90﹣8t)+4×6t=270°.
即3∠NOD+4∠BOM=270°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数n都可以进行这样的分解:
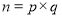 (p,q是正整数,且
(p,q是正整数,且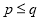 ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定: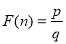 .
.例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=
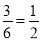 .
.(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为
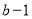 ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;(3)在(2)所得“和谐数”中,求F(t)的最大值.
-
科目: 来源: 题型:
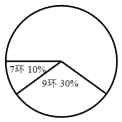
查看答案和解析>>【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
命中环数
10
9
8
7
命中次数
3
2
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据《南昌晚报》2019 年 4 月 28 日报道,“五一”期间南昌天气预报气温如下:
时间
4 月 29 日
4 月 30 日
5 月 1 日
5 月 2 日
5 月 3 日
最低气温
18℃
18℃
19℃
18℃
19℃
最高气温
22℃
24℃
27℃
22℃
24℃
则“五一”期间南昌天气预报气温日温差最大的时间是( )
A. 4 月 29 日B. 4 月 30 日C. 5 月 1 日D. 5 月 3 日
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
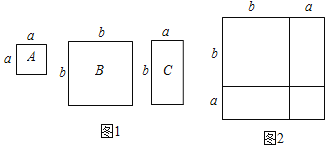
(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称次抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点的横坐标为﹣1,求“带线”L的表达式;
(2)如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系,求m,n的值;
(3)设(2)中的“带线”L与它的“路线”l在y轴上的交点为A.已知点P为“带线”L上的点,当以点P为圆心的圆与“路线”l相切于点A时,求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2013次输出的结果为( )
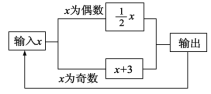
A.6B.3C.
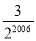 D.
D.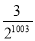 +3×1003
+3×1003
相关试题

