【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称次抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点的横坐标为﹣1,求“带线”L的表达式;
(2)如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系,求m,n的值;
(3)设(2)中的“带线”L与它的“路线”l在y轴上的交点为A.已知点P为“带线”L上的点,当以点P为圆心的圆与“路线”l相切于点A时,求出点P的坐标.
参考答案:
【答案】(1)“带线”L的表达式为y=2x2+4x﹣4;(2)m=2,n=﹣2;(3)点P的坐标为(![]() ,
, ![]() ).
).
【解析】试题分析:
(1)由“路线l”的表达式为:y=2x-4可得,“路线l”与y轴交于点(0,-4);把x=-1代入y=2x-4可得y=-6,由此可得“带线L”的顶点坐标为(-1,-6),结合“带线L”过点(0,-4)即可求得“带线L”的解析式;
(2)由y=mx2﹣2mx+m﹣1=m(m-1)2-1可得“带线L”的顶点坐标为(1,-1),与y轴交于点(0,m-1),把这两个点的坐标代入y=nx+1即可求得m、n的值;
(3)如图,由(2)可知,若设“带线L”的顶点为B,则点B坐标为(1,﹣1),过点B作BC⊥y轴于点C,连接PA并延长交x轴于点D,由⊙P与“路线”l相切于点A可得PD⊥l于点A,由此证Rt△AOD≌Rt△BCA即可求得点D的坐标,结合点A的坐标即可求得AD的解析式为y=![]() x+1,由AD的解析式和“带线L”的解析式组成方程组,解方程组即可求得点P的坐标.
x+1,由AD的解析式和“带线L”的解析式组成方程组,解方程组即可求得点P的坐标.
试题解析:
((1)∵“带线”L的顶点横坐标是﹣1,且它的“路线”l的表达式为y=2x﹣4
∴y=2×(﹣1)﹣4=﹣6,
∴“带线”L的顶点坐标为(﹣1,﹣6).
设L的表达式为y=a(x+1)2﹣6,
∵“路线”y=2x﹣4与y轴的交点坐标为(0,﹣4)
∴“带线”L也经过点(0,﹣4),将(0,﹣4)代入L的表达式,解得a=2
∴“带线”L的表达式为 y=2(x+1)2﹣6=2x2+4x﹣4;
(2)∵直线y=nx+1与y轴的交点坐标为(0,1),
∴抛物线y=mx2﹣2mx+m﹣1与y轴的交点坐标也为(0,1),解得m=2,
∴抛物线表达式为y=2x2﹣4x+1,其顶点坐标为(1,﹣1)
∴直线y=nx+1经过点(1,﹣1),解得n=﹣2;
(3)如图,设“带线L”的顶点为B,则点B坐标为(1,﹣1),过点B作BC⊥y轴于点C,
∴∠BCA=90°,
又∵点A 坐标为(0,1),
∴AO=1,BC=1,AC=2.
∵“路线”l是经过点A、B的直线
且⊙P与“路线”l相切于点A,连接PA交 x轴于点D,
∴PA⊥AB,
∴∠DAB=∠AOD=90°,
∴∠ADO+∠DAO=90°,
又∵∠DAO+∠BAC=90°,
∴∠ADO=∠BAC,
∴Rt△AOD≌Rt△BCA,
∴OD=AC=2,
∴D点坐标为(﹣2,0)
∴经过点D、A的直线表达式为y=![]() x+1,
x+1,
∵点P为直线y=![]() x+1与抛物线L:y=2x2﹣4x+1的交点,
x+1与抛物线L:y=2x2﹣4x+1的交点,
解方程组: 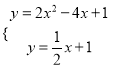 得 :
得 : ![]() (即点A舍去),
(即点A舍去),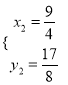 ,
,
∴点P的坐标为![]() .
.
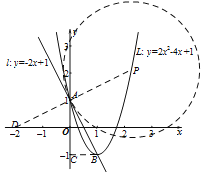
-
科目: 来源: 题型:
查看答案和解析>>【题目】据《南昌晚报》2019 年 4 月 28 日报道,“五一”期间南昌天气预报气温如下:
时间
4 月 29 日
4 月 30 日
5 月 1 日
5 月 2 日
5 月 3 日
最低气温
18℃
18℃
19℃
18℃
19℃
最高气温
22℃
24℃
27℃
22℃
24℃
则“五一”期间南昌天气预报气温日温差最大的时间是( )
A. 4 月 29 日B. 4 月 30 日C. 5 月 1 日D. 5 月 3 日
-
科目: 来源: 题型:
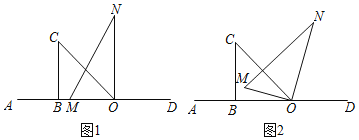
查看答案和解析>>【题目】将一副直角三角板按如图1摆放在直线AD上
 直角三角板OBC和直角三角板MON,
直角三角板OBC和直角三角板MON,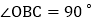 ,
,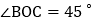 ,
,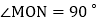 ,
, ,保持三角板OBC不动,将三角板MON绕点O以每秒
,保持三角板OBC不动,将三角板MON绕点O以每秒 的速度顺时针方向旋转t秒
的速度顺时针方向旋转t秒
 如图2,
如图2,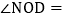 ______度
______度 用含t的式子表示
用含t的式子表示 ;
; 在旋转的过程中,是否存在t的值,使
在旋转的过程中,是否存在t的值,使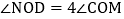 ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由. 直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒
直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒 的速度顺时针旋转.
的速度顺时针旋转. 当
当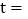 ______秒时,
______秒时,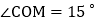 ;
; 请直接写出在旋转过程中,
请直接写出在旋转过程中, 与
与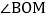 的数量关系
的数量关系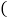 关系式中不能含
关系式中不能含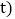 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
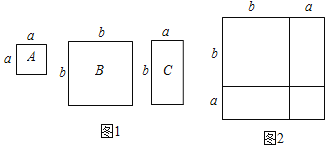
(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
-
科目: 来源: 题型:
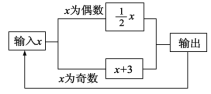
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2013次输出的结果为( )
A.6B.3C.
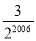 D.
D.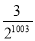 +3×1003
+3×1003 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为2,D、E分别是边AB、AC上的点,沿DE所在的直线折叠∠A,使点A的对应点P始终落在边BC上,若△BDP是直角三角形,则AD的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列填空:
(1)如图,
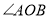 为直角,
为直角,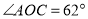 ,且
,且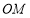 平分
平分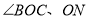 平分
平分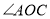 ,求
,求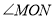 的度数.
的度数.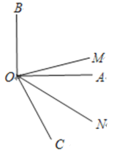
(2)如图,
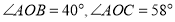 ,且
,且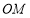 平分
平分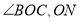 平分
平分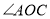 .直接写出
.直接写出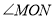 的度数.
的度数.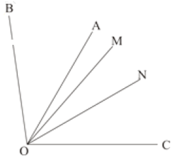
解:(1)因为
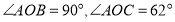 ,所以
,所以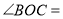 ①
① 
因为
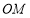 平分
平分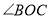 ,所以
,所以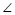 ②
② 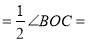 ③
③ 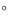
因为
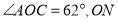 平分
平分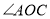 ,所以
,所以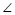 ④
④ 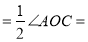 ⑤
⑤ 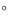
所以
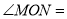 ⑥
⑥ 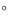
(2)
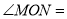 ⑦
⑦ 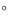
相关试题

