【题目】为调查七年级某班学生每天完成家庭作业所需的时间,在该班随机抽查了8名学生,他们每天完成作业所需时间(单位:分)分别为:60,55,75,55,55,43,65,40.
(1)求这组数据的众数、中位数;
(2)求这8名学生每天完成家庭作业的平均时间;如果按照学校要求,学生每天完成家庭作业时间不能超过60分钟,问该班学生每天完成家庭作业的平均时间是否符合学校的要求?
参考答案:
【答案】(1)55;55;(2) 符合学校的要求.
【解析】试题分析:(1)用众数、中位数、平均数的定义去解.
(2)求出这8名学生每天完成家庭作业的平均时间.把这个样本的平均数与60分钟进行比较就可以.
试题解析:(1)在这8个数据中,55出现了3次,出现的次数最多,即这组数据的众数是55;将这8个数据按从小到大的顺序排列,其中最中间的两个数据都是55,即这组数据的中位数是55.
(2)这8个数据的平均数是![]() (60+55×3+75+43+65+40)=56(分).
(60+55×3+75+43+65+40)=56(分).
∴这8名学生完成家庭作业的平均时间为56分钟,
因为56<60,
因此估计该班学生每天完成家庭作业的平均时间符合学校的要求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一组数据1,2,3,4,x的平均数与中位数相同,则实数x的值不可能
 是( )
是( )A. 0 B. 2.5 C. 3 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程时,配方正确的是( )
A.方程x2﹣6x﹣5=0,可化为(x﹣3)2=4
B.方程y2﹣2y﹣2015=0,可化为(y﹣1)2=2015
C.方程a2+8a+9=0,可化为(a+4)2=25
D.方程2x2﹣6x﹣7=0,可化为

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
(1)求出b、c的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值y为正数时,自变量x的取值范围;
(3)当2≤x≤4时,求y的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市射击队为了从甲、 乙 两名运动员中选出一名运动员参加省运动会比赛,组织了选拔测试,两人分别进行了五次射击,成绩(单位:环)如下:
甲
10
9
8
9
9
乙
10
8
9
8
10
你认为应选择哪位运动员参加省运动会比赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将有一30度角的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°)

(1)将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90°
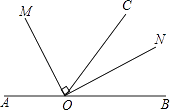
(1)求∠BOM的度数;
(2)ON是∠BOC的角平分线吗?请说明理由.
相关试题

