【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将有一30度角的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°) 
(1)将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
参考答案:
【答案】
(1)解:直线ON平分∠AOC;
理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB=60°,
又∵OM⊥ON,
∴∠MON=90°,
∴∠BON=30°,
∴∠CON=120°+30°=150°,
∴∠COD=30°,
∴OD平分∠AOC,
即直线ON平分∠AOC
(2)解:由(1)可知∠BON=30°,∠DON=180°
因此ON旋转60°或240°时直线ON平分∠AOC,
由题意得,6t=60°或240°,
∴t=10或40
(3)解:∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°
【解析】(1)由角的平分线的定义和等角的余角相等求解;(2)由∠BOC=120°可得∠AOC=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解;(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,然后作差即可.
【考点精析】掌握角的平分线和余角和补角的特征是解答本题的根本,需要知道从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;互余、互补是指两个角的数量关系,与两个角的位置无关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
(1)求出b、c的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值y为正数时,自变量x的取值范围;
(3)当2≤x≤4时,求y的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为调查七年级某班学生每天完成家庭作业所需的时间,在该班随机抽查了8名学生,他们每天完成作业所需时间(单位:分)分别为:60,55,75,55,55,43,65,40.
(1)求这组数据的众数、中位数;
(2)求这8名学生每天完成家庭作业的平均时间;如果按照学校要求,学生每天完成家庭作业时间不能超过60分钟,问该班学生每天完成家庭作业的平均时间是否符合学校的要求?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市射击队为了从甲、 乙 两名运动员中选出一名运动员参加省运动会比赛,组织了选拔测试,两人分别进行了五次射击,成绩(单位:环)如下:
甲
10
9
8
9
9
乙
10
8
9
8
10
你认为应选择哪位运动员参加省运动会比赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90°
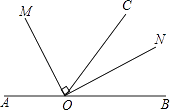
(1)求∠BOM的度数;
(2)ON是∠BOC的角平分线吗?请说明理由. -
科目: 来源: 题型:
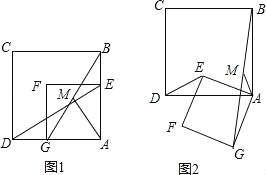
查看答案和解析>>【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形.
(1)如图1,连接DE,BG,M为线段BG的中点,连接AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】亚洲陆地面积约为4400万平方千米,将44000000用科学记数法表示为( )
A. 44×106B. 4.4×107C. 4.4×108D. 0.44×108
相关试题

