【题目】如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=度.
参考答案:
【答案】46
【解析】解:∵∠A=27°,∠B=40°,
∴∠ACA′=∠A+∠B=27°+40°=67°,
∵△ABC绕点C按顺时针方向旋转至△A′B′C,
∴△ABC≌△A′B′C,
∴∠ACB=∠A′CB′,
∴∠ACB﹣∠B′CA=∠A′CB﹣∠B′CA,
即∠BCB′=∠ACA′,
∴∠BCB′=67°,
∴∠ACB′=180°∠ACA′﹣∠BCB′=180°﹣67°﹣67°=46°,
故答案为:46.
先根据三角形外角的性质求出∠ACA′=67°,再由△ABC绕点C按顺时针方向旋转至△A′B′C,得到△ABC≌△A′B′C,证明∠BCB′=∠ACA′,利用平角即可解答.本题考查了旋转的性质,解决本题的关键是由旋转得到△ABC≌△A′B′C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )

A.y=x+5
B.y=x+10
C.y=﹣x+5
D.y=﹣x+10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( )
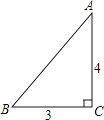
A.c>a>b
B.b>a>c
C.c>b>a
D.b>c>a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
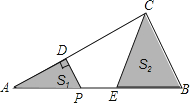
A.一直减小
B.一直不变
C.先减小后增大
D.先增大后减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的
 时,求出这时点M的坐标.
时,求出这时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在反比例函数y=
 (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 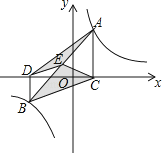
相关试题

