【题目】如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( ) 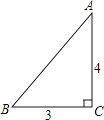
A.c>a>b
B.b>a>c
C.c>b>a
D.b>c>a
参考答案:
【答案】D
【解析】解:第一次折叠如图1,折痕为DE,由折叠得:AE=EC= ![]() AC=
AC= ![]() ×4=2,DE⊥AC
×4=2,DE⊥AC
∵∠ACB=90°
∴DE∥BC
∴a=DE= ![]() BC=
BC= ![]() ×3=
×3= ![]()
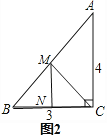
第二次折叠如图2,折痕为MN,
由折叠得:BN=NC= ![]() BC=
BC= ![]() ×3=
×3= ![]() ,MN⊥BC
,MN⊥BC
∵∠ACB=90°
∴MN∥AC
∴b=MN= ![]() AC=
AC= ![]() ×4=2
×4=2
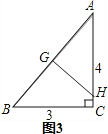
第三次折叠如图3,折痕为GH,
由勾股定理得:AB= ![]() =5由折叠得:AG=BG=
=5由折叠得:AG=BG= ![]() AB=
AB= ![]() ×5=
×5= ![]() ,GH⊥AB
,GH⊥AB
∴∠AGH=90°
∵∠A=∠A,∠AGH=∠ACB
∴△ACB∽△AGH
∴ ![]() =
= ![]() ∴
∴ ![]() =
= ![]() ∴GH=
∴GH= ![]() ,即c=
,即c= ![]() ∵2>
∵2> ![]() >
> ![]()
∴b>c>a
故选D.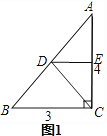
(1)图1,根据折叠得:DE是线段AC的垂直平分线,由中位线定理的推论可知:DE是△ABC的中位线,得出DE的长,即a的长;
(2)图2,同理可得:MN是△ABC的中位线,得出MN的长,即b的长;
(3)图3,根据折叠得:GH是线段AB的垂直平分线,得出AG的长,再利用两角对应相等证△ACB∽△AGH,利用比例式可求GH的长,即c的长.本题考查了折叠的问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.本题的关键是明确折痕是所折线段的垂直平分线,准确找出中位线,利用经过三角形一边中点与另一边平行的直线必平分第三边这一性质得出对应折痕的长,没有中位线的可以考虑用三角形相似来解决.
-
科目: 来源: 题型:
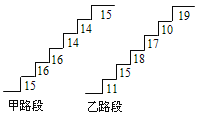
查看答案和解析>>【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识,回答下列问题(数据:15,16,16,14,14,15的方差
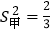 ,数据:11,15,18,17,10,19的方差
,数据:11,15,18,17,10,19的方差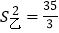 :
:(1)分别求甲、乙两段台阶的高度平均数;
(2)哪段台阶走起来更舒服?与哪个数据(平均数、中位数、方差和极差)有关?
(3)为方便游客行走,需要陈欣整修上山的小路,对于这两段台阶路.在总高度及台阶数不变的情况下,请你提出合理的整修建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
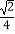 x2﹣2x﹣6
x2﹣2x﹣6 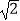 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点,点E在抛物线上,且横坐标为4
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点,点E在抛物线上,且横坐标为4 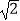 ,AE与y轴交F.
,AE与y轴交F.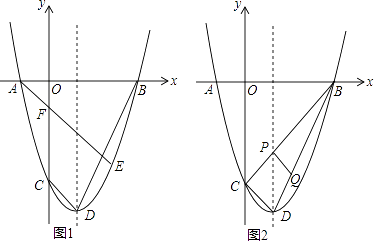
(1)求抛物线的顶点D和F的坐标;
(2)点M,N是抛物线对称轴上两点,且M(2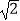 ,a),N(2
,a),N(2 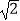 ,a+
,a+ 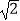 ),是否存在a使F,C,M,N四点所围成的四边形周长最小,若存在,求出这个周长最小值,并求出a的值;
),是否存在a使F,C,M,N四点所围成的四边形周长最小,若存在,求出这个周长最小值,并求出a的值;
(3)连接BC交对称轴于点P,点Q是线段BD上的一个动点,自点D以2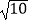 个单位每秒的速度向终点B运动,连接PQ,将△DPQ沿PQ翻折,点D的对应点为D′,设Q点的运动时间为t(0≤t≤
个单位每秒的速度向终点B运动,连接PQ,将△DPQ沿PQ翻折,点D的对应点为D′,设Q点的运动时间为t(0≤t≤ 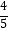 )秒,求使得△D′PQ与△PQB重叠部分的面积为△DPQ面积的
)秒,求使得△D′PQ与△PQB重叠部分的面积为△DPQ面积的  时对应的t值.
时对应的t值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )

A.y=x+5
B.y=x+10
C.y=﹣x+5
D.y=﹣x+10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
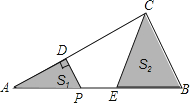
A.一直减小
B.一直不变
C.先减小后增大
D.先增大后减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的
 时,求出这时点M的坐标.
时,求出这时点M的坐标.
相关试题

