【题目】根据市卫生防疫部门的要求,游泳池必须定期换水后才能对外开放.在换水时需要经“排水—清冼—灌水”的过程.某游泳馆从早上7:00开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的1.6倍,其中游泳池内剩余的水量y(m3)与换水时间x(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)填空:该游泳池清洗需要 小时;
(2)求排水过程中的y(m3)与x(h)之间的函数关系式,并写出自变量x的取值范围;
(3)若该游泳馆在换水结束后30分钟才能对外开放,试问游泳爱好者小明能否在中午12:40进入该游泳馆游泳?

参考答案:
【答案】(1)1.2;(2)排水过程中的y与x之间的函数关系式为:y=-800x+1200(0≤x≤1.5);(3)游泳爱好者小明能在中午12:40进入该游泳馆游泳.
【解析】
(1)根据函数图象中的数据可以解答本题;
(2)根据题意核函数图象中的数据可以求得排水过程中的V(m3)与t(h)之间的函数关系式,并写出自变量t的取值范围;
(3)根据题意可以求得下午几点开放,然后与13:30比较大小即可解答本题.
(1)由题意可得,该游泳池清洗需要:2.7﹣1.5=1.2(小时),故答案为:1.2;
(2)设排水过程中的y(m3)与x(h)之间的函数关系式为:y=kx+b,由题知
![]() ,解得
,解得![]() ,∴排水过程中的y与x之间的函数关系式为:
,∴排水过程中的y与x之间的函数关系式为:
y=-800x+1200(0≤x≤1.5);
(3)由题意可得,排水的速度为:1200÷1.5=800(m3/h),
∴灌水的速度为:800÷1.6=500(m3/h),∴灌水用的时间为:1200÷500=2.4h,
∴对外开放的时间为:7+2.7+2.4+![]() =12.6<12
=12.6<12![]() ,
,
∴游泳爱好者小明能在中午12:40进入该游泳馆游泳.
-
科目: 来源: 题型:
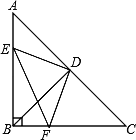
查看答案和解析>>【题目】已知:如图,在△ABC中,∠ABC=90°,AB=BC,D是AC的中点,点E在AC上,点F在BC上,且AE=BF.
(1)求证:DE=DF;
(2)连接EF,求∠DEF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
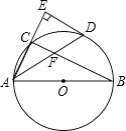
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.
(1)求证:四边形AECF是平行四边形;
(2)如果AE=3,EF=4,求AF、EC所在直线的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(2﹣π)0+(
 )﹣2+(﹣2)3
)﹣2+(﹣2)3 (2)(﹣3a6)2﹣a22a10+(﹣2a2)3a3
(3)(x+1)2﹣(1﹣2x)(1+2x)
(4)(x+2)(x﹣3)﹣x(x+1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断AC与DF的位置关系,并说明理由;
(2)若∠C比∠A大20°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=6cm,AC=12cm,动点D以1cm/s 的速度从点A出发到点B止,动点E以2cm/s 的速度从点C出发到点A止,且两点同时运动,当以点A、D、E为顶点的三角形与△ABC相似时,求运动的时间t.

相关试题

