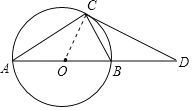
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.

参考答案:
【答案】(1)证明见解析(2)2
【解析】
试题分析:(1)连接OC,由AB是⊙O的直径可得出∠ACB=90°,即∠ACO+∠OCB=90°,由等腰三角形的性质结合∠BCD=∠A,即可得出∠OCD=90°,即CD是⊙O的切线;
(2)在Rt△OCD中,由勾股定理可求出OD的值,进而可得出BD的长.
试题解析:(1)如图,连接OC.
∵AB是⊙O的直径,C是⊙O上一点,
∴∠ACB=90°,即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,
∴∠ACO=∠A=∠BCD,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴CD是⊙O的切线.
(2)在Rt△OCD中,∠OCD=90°,OC=3,CD=4,
∴OD=![]() =5,
=5,
∴BD=OD﹣OB=5﹣3=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,直线y=x+m和抛物线y=
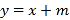 +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),B(3,2).
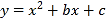
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
-
科目: 来源: 题型:
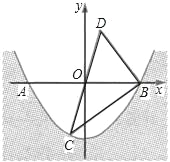
查看答案和解析>>【题目】某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2﹣4.
(1)求a的值;
(2)点C(﹣1,m)是抛物线上一点,点C关于原点O的对称点为点D,连接CD,BC,BD,求△BCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校欲招聘一名新教师,对甲、乙、丙三名应试者进行了面试、笔试和才艺三个方面的量化考核,他们的各项得分(百分制)如下表所示:
应试者
面试成绩
笔试成绩
才艺
甲
83
79
90
乙
85
80
75
丙
80
90
73
(1)根据三项得分的平均分,从高到低确定应聘者的排名顺序;
(2)学校规定:笔试、面试、才艺得分分别不得低于80分、80分、70分,并按照60%、30%、10%的比例计入个人总分,请你说明谁会被录用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,与直线
,与直线 交于点
交于点 ,点
,点 的横坐标为3.
的横坐标为3.
(1)直接写出
 值________;
值________;(2)当
 取何值时,
取何值时, ?
?(3)在
 轴上有一点
轴上有一点 ,过点
,过点 作
作 轴的垂线,与直线
轴的垂线,与直线 交于点
交于点 ,与直线
,与直线 交于点
交于点 ,若
,若 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】希腊数学家丢番图(公元3-4世纪)的墓碑上记载着: “他生命的六分之一是幸福的童年;再活了他生命的十二分之一,两颊长起了细细的胡须;他结了婚,又度过了一生的七分之一;再过五年,他有了儿子,感到很幸福;可是儿子只活了他父亲全部年龄的一半;儿子死后,他在极度悲痛中度过了四年,也与世长辞了.”
根据以上信息,请你算出:
(1)丢番图的寿命;
(2)丢番图开始当爸爸时的年龄;
(3)儿子死时丢番图的年龄.
相关试题

