【题目】2017年11月11日,张杰参加了某网点的“翻牌抽奖”活动.如图所示,4张牌上分别写有对应奖品的价值为10元,15元,20元和“谢谢惠顾”的字样.
⑴如果随机翻1张牌,那么抽中有奖的概率为 ,抽中15元及以上奖品的概率为 .
⑵如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,用画树状图或列表法列出抽奖的所有等可能性情况,并求出获奖品总值不低于30元的概率.

参考答案:
【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数,据此计算,求出抽中有奖和15元以上奖品的概率为多少即可;
(2)首先应用树状图法,列举出随机翻2张牌,所获奖品的总值一共有多少种情况;然后用所获奖品总值不低于30元的情况的数量除以所有情况的数量,求出所获奖品总值不低于30元的概率为多少即可.
解:(1)3÷4=![]() ,1÷2=
,1÷2=![]() ,
,
∴抽中奖的概率为![]() ,抽中15元及以上的概率为
,抽中15元及以上的概率为![]() ;
;
故答案为: ![]() ;
; ![]() ;
;
(2) 画出树状图得:

∴由树状图可知,一共有12种等可能性的抽奖结果;其中总值不低于30元的有4种情况. 所获奖品总值不低于30元的概率=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D 的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
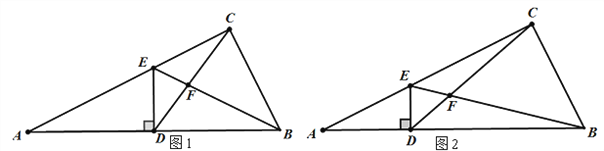
查看答案和解析>>【题目】如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F.若tanA=
 ,则
,则 =_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若
=_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若 ,tanA=
,tanA= ,则
,则 =____.
=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片ABCD放在每格宽度都为6mm的横格纸中,恰好四个顶点都在横格线上,已知a=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】元旦前夕,湖州吴兴某工艺厂设计了一款成本10元/件的工艺品投放市场试销.试销发现,每天销售量y(件)与销售单价x(元/件)之间的关系可近似地看作一次函数:y=-10x+700. (利润=销售总价-成本总价)
⑴ 如果该厂想要每天获得5000元的利润,那么销售单价应定为多少元/件?
⑵ 当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
⑶ 湖州市物价部门规定,该工艺品销售单价最高不能超过38元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部△CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(1)当MN和AB之间的距离为0.5米时,求此时△EMN的面积;
(2)设MN与AB之间的距离为x 米,试将△EMN的面积S(平方米)表示成关于x的函数;
(3)请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.

相关试题

