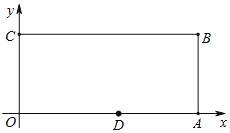
【题目】如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
参考答案:
【答案】6或7或12或14
【解析】
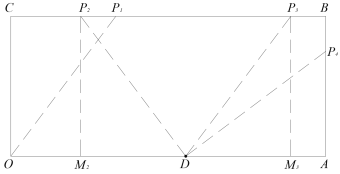
当OP=OD时,可得P1点;当DP=OD时,可得P2、P3、P4三种情况,再运用勾股定理可分别求解.
解:当OP=OD时,可得P1点,此时由勾股定理可得,OC2+CP12=OP12,即42+CP12=52,解得CP1=3,则t=![]() 秒;
秒;
当DP=OD时,可得P2、P3、P4三种情况,当P点运动到P2位置时,作P2M2⊥OA,由勾股定理可得,P2M22+ DM22=DP22,即42+ DM22=52,解得DM2=3,同理可解得DM3=AP4=3,
故,当P点运动到P2位置时,t=![]() 秒;当P点运动到P3位置时,t=
秒;当P点运动到P3位置时,t=![]() 秒;当P点运动到P4位置时,t=
秒;当P点运动到P4位置时,t=![]() 秒;
秒;
故答案为:6或7或12或14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:若
 ,求m、n的值.
,求m、n的值.解:∵
 ,
,∴
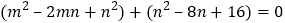
∴
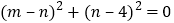 ,而
,而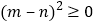 ,
,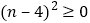 ,
, ∴
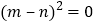 且
且 ,
,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)
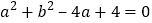 ,则a=______;b=_________.
,则a=______;b=_________.(2)已知△ABC的三边a,b,c满足
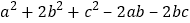 =0,
=0,关于此三角形的形状的以下命题:①它是等边三角形;②它属于等腰三角形:③它属于锐角三角形;④它不是直角三角形.其中所有正确命题的序号为________________.
(3)已知△ABC的三边长a、b、c都是正整数,且
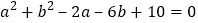 ,求△ABC的周长.
,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠A=40°.点P是射线AB上一动点(与点A不重合),CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F.
(1)求∠ECF的度数;
(2)随着点P的运动,∠APC与∠AFC之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由;
(3)当∠AEC=∠ACF时,求∠APC的度数.

-
科目: 来源: 题型:
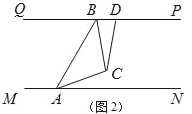
查看答案和解析>>【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值.
(2)若一条直线经过A(2,3),且与y=
 x+3垂直,求这条直线的函数关系式.
x+3垂直,求这条直线的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l和双曲线
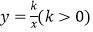 交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 , 则( )
交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 , 则( )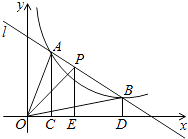
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )

A.6cm2
B.8cm2
C.10cm2
D.12cm2
相关试题

