搜索
【题目】已知，如图，矩形ABCD中，AB=3cm，AD=9cm，将此矩形折叠，使点D与点B重合，折痕为EF，则△ABE的面积为（ ）
A.6cm2
B.8cm2
C.10cm2
D.12cm2
参考答案：
【答案】A
【解析】将此长方形折叠，使点B与点D重合，
∴BE=ED．
∵AD=AE+DE=AE+BE=9（cm）．
∴BE=9﹣AE，
根据勾股定理可知AB2+AE2=BE2．
解得AE=4．
∴△ABE的面积为 
×3×4=6（cm2）．
所以答案是：A．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A、C、D的坐标分别为A(9，0)、C(0，4)，D(5，0)，点P从点O出发，以每秒1个单位长度的速度沿O→C→B→A运动，点P的运动时间为t秒．则当t＝____秒时，△ODP是腰长为5的等腰三角形？
-
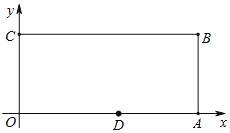
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：已知两直线，L1：y＝k1x+b1，L2：y＝k2x+b2，若L1⊥L2，则有k1k2＝﹣1，根据以上结论解答下列各题：
(1)已知直线y＝2x+1与直线y＝kx﹣1垂直，求k的值．
(2)若一条直线经过A(2，3)，且与y＝
x+3垂直，求这条直线的函数关系式． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l和双曲线
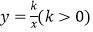交于A，B两点，P是线段AB上的点（不与A，B重合），过点A，B，P分别向x轴作垂线，垂足分别为C，D，E，连接OA，OB，0P，设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 ， 则（ ）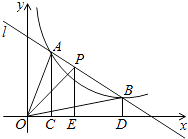
A.S1＜S2＜S3
B.S1＞S2＞S3
C.S1=S2＞S3
D.S1=S2＜S3 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，有若干个整数点(横、纵坐标均为整数)，其顺序按图中方向排列，如(1，0)，(2，0)，(2，1)，(3，1)，(3，0)…… 根据这个规律探索可得，第50个点的坐标为（ ）
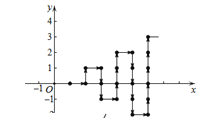
A. (10，－5)B. (10，－1) C. (10，0) D. (10，1）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图1，在平面直角坐标系中，一次函数y＝
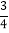x+3交x轴于点A，交y轴于点B，点C是点A关于y轴对称的点，过点C作y轴平行的射线CD，交直线AB与点D，点P是射线CD上的一个动点．(1)求点A，B的坐标．
(2)如图2，将△ACP沿着AP翻折，当点C的对应点C′落在直线AB上时，求点P的坐标．
(3)若直线OP与直线AD有交点，不妨设交点为Q(不与点D重合)，连接CQ，是否存在点P，使得S△CPQ＝2S△DPQ，若存在，请求出对应的点Q坐标；若不存在，请说明理由．
-
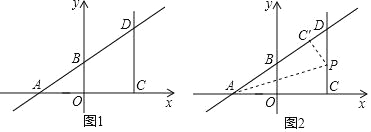
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的证明
如图，FG//CD，∠1=∠3，∠B=50°，求∠BDE的度数.
解：∵FG//CD (已知)
∴∠2=_________（____________________________）
又∵∠1=∠3，
∴∠3=∠2（等量代换）
∴BC//__________（_____________________________）
∴∠B+________=180°（______________________________）
又∵∠B=50°
∴∠BDE=________________.
相关试题
