【题目】已知![]() 的一条边
的一条边![]() 的长为5,另两边
的长为5,另两边![]() 的长是关于
的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根.
的两个实数根.
(1)求证:无论![]() 为何值,方程总有两个不相等的实数根;
为何值,方程总有两个不相等的实数根;
(2)当![]() 为何值时,
为何值时,![]() 为直角三角形,并求出
为直角三角形,并求出![]() 的周长.
的周长.
参考答案:
【答案】(1)证明见解析;(2)当![]() 时,周长为12,当
时,周长为12,当![]() 时,周长为30.
时,周长为30.
【解析】
(1)要证明无论k为何值时,方程总有两个不相等的实数根,就是证明△>0,求出的值即可;
(2)先用含k的代数式表示出方程的两个根,再分两种情况求解即可.
(1)证明:![]()
![]()
![]() ,
,
![]() 无论
无论![]() 为何值,方程总有两个不相等的实数根.
为何值,方程总有两个不相等的实数根.
(2)![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
由于![]() ,故分两种情况讨论:
,故分两种情况讨论:
①当![]() 为斜边时,
为斜边时,![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
则![]() ,
,![]() ,
,
此时,![]() 的周长为
的周长为![]() ;
;
②当![]() 是斜边时,
是斜边时,![]() ,
,
解得![]() ,
,
则![]() ,
,,
此时,![]() 的周长为
的周长为![]() .
.
综上可知,当![]() 时,周长为12,当
时,周长为12,当![]() 时,周长为30.
时,周长为30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )

A. ①② B. ①③ C. ①④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数
 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于
的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于  ,其中正确的个数有( )
,其中正确的个数有( )
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCE的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,则△MAN的面积的最小值为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0)、A(0,6)、B(4,6)、C(4,4)、D(6,4),E(6,0),若直线L经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线L的函数表达式是

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△AEF的顶点E,F分别在BC、CD边上,高AG与正方形的边长相等,连BD分别交AE、AF于点M、N,若EG=4,GF=6,BM=
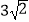 ,则MN的长为。
,则MN的长为。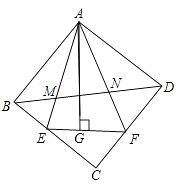
相关试题

