【题目】如图,在正方形ABCD中,△AEF的顶点E,F分别在BC、CD边上,高AG与正方形的边长相等,连BD分别交AE、AF于点M、N,若EG=4,GF=6,BM= ![]() ,则MN的长为。
,则MN的长为。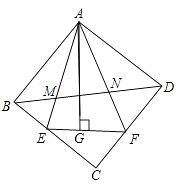
参考答案:
【答案】![]()
【解析】解:如图,连接GM,GN,
∵AG=AB,AE=AE,
∴△AGE≌△ABE,
同理可证△AGF≌△ADF,
∴BE=EG=4,DF=FG=6,
设正方形的边长为a,在Rt△CEF中,CE=a-4,CF=a-6,
由勾股定理,得CE2+CF2=EF2 , 即(a-4)2+(a-6)2=102 ,
解得a=12或-2(舍去负值),
∴BD=12 ![]() , 易证△ABM≌△AGM,△ADN≌△AGN,
, 易证△ABM≌△AGM,△ADN≌△AGN,
∴MG=BM=3 ![]() ,NG=ND=1
,NG=ND=1 ![]() -3
-3 ![]() -MN=9
-MN=9 ![]() -MN, ∠MGN=∠MGA+∠NGA=∠MBA+∠NDA=90°,
-MN, ∠MGN=∠MGA+∠NGA=∠MBA+∠NDA=90°,
在Rt△GMN中,由勾股定理,得MG2+NG2=MN2 , 即(3 ![]() )2+(9
)2+(9 ![]() -MN)2=MN2 ,
-MN)2=MN2 ,
解得MN=5 ![]()
所以答案是:5 ![]() .
.
【考点精析】通过灵活运用勾股定理的概念,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的一条边
的一条边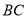 的长为5,另两边
的长为5,另两边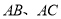 的长是关于
的长是关于 的一元二次方程
的一元二次方程 的两个实数根.
的两个实数根.(1)求证:无论
 为何值,方程总有两个不相等的实数根;
为何值,方程总有两个不相等的实数根;(2)当
 为何值时,
为何值时, 为直角三角形,并求出
为直角三角形,并求出 的周长.
的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0)、A(0,6)、B(4,6)、C(4,4)、D(6,4),E(6,0),若直线L经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线L的函数表达式是

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= ( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=
 ( )
( )∠ABE=
 ( )
( )∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠DEB.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
 中,动点
中,动点 在
在 边上,以每秒
边上,以每秒 的速度从点
的速度从点 向点
向点 运动.
运动.(1)如图1,在运动过程中,若
 平分
平分 ,且满足
,且满足 ,求
,求 的度数.
的度数.(2)如图2,在(1)的条件下,连结
 并延长与
并延长与 的延长线交于点
的延长线交于点 ,连结
,连结 ,若
,若 ,求
,求 的面积.
的面积.(3)如图3,另一动点
 在
在 边上,以每秒
边上,以每秒 的速度从点
的速度从点 出发,在
出发,在 间往返运动,
间往返运动, 两点同时出发,当点
两点同时出发,当点 到达点
到达点 时停止运动(同时
时停止运动(同时 点也停止),若
点也停止),若 ,求当运动时间为多少秒时,以D,四点组成的四边形是平行四边形.
,求当运动时间为多少秒时,以D,四点组成的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
(1)写出点A、B的坐标:A(_____,_____)、B(_____,_____);
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,写出A′、B′、C′三点坐标;
(3)求△ABC的面积。

相关试题

