【题目】用甲、乙两种原料配制某种饮料,这两种原料的维生素C含量及购买两种原料的价格如表:
原料 | 甲 | 乙 |
维生素C的含量/(单位/kg) | 600 | 100 |
原料价格/(元/kg) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,且购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量应满足的范围.
参考答案:
【答案】解:需用x千克甲种原料,则需乙种原料(10﹣x)千克,
依题意得: 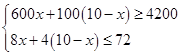 ;
;
由第一个不等式变形得:600x+1000﹣100x≥4200,
整理得:500x≥3200,
解得:x≥6.4,
由第二个不等式变形得:8x+40﹣4x≤72,
整理得:4x≤32,
解得:x≤8,
可得6.4≤x≤8.
【解析】需用x千克甲种原料,则需乙种原料(10﹣x)千克,根据“甲、乙两种原料的费用不超过72元”和“至少含有4200单位的维生素C”列不等式组,解不等式组即可求解.
【考点精析】本题主要考查了一元一次不等式组的应用的相关知识点,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能正确解答此题.
-
科目: 来源: 题型:
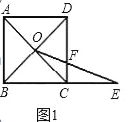
查看答案和解析>>【题目】数学课上,张老师出示了问题1:如图1,四边形ABCD是正方形,BC=1,对角线交点记作O,点E是边BC延长线上一点.连接OE交CD边于F,设CE=x,CF=y,求y关于x的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线﹣﹣过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
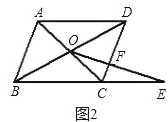
(2)如果将问题1中的条件“四边形ABCD是正方形,BC=1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;
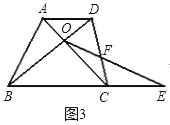
(3)如果将问题1中的条件“四边形ABCD是正方形,BC=1”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c(其中a,b,c为常量)”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求式子中x的值:4(x﹣1)2﹣16=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于-3而小于2的所有整数的和是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)解方程:x2﹣4x﹣3=0
(2)解不等式组: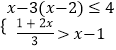 并将解集在数轴上表示出来.
并将解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+1)2+|y-3|=0,则xy=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
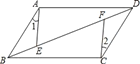
A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
相关试题

