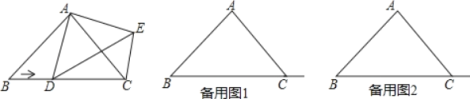
【题目】已等腰Rt△ABC中,∠BAC=90°.点D从点B出发沿射线BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.
(1)如图,求证:△ACE≌△ABD;
(2)点D运动时,∠BCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3)若AC=![]() ,当CD=1时,请直接写出DE的长.
,当CD=1时,请直接写出DE的长.
参考答案:
【答案】(1)证明见解析;(2)∠BCE的度数不变,为90°;(3)DE的长为![]() 或
或![]() .
.
【解析】
(1)由△ABC和△ADE都是等腰Rt△可得,AB=AC,AD=AE,∠BAC=∠DAE=90°,则有∠BAD=∠CAE,从而可证到△ACE≌△ABD;
(2)由△ACE≌△ABD可得∠ACE=∠ABD=45°,从而得到∠BCE=∠BCA+∠ACE=90°;
(3)可分点D在线段BC上时(如图1)和点D在线段BC延长线上时(如图2)两种情况讨论,在Rt△ABC中运用勾股定理可求出BC,从而得到BD,由△ACE≌△ABD可得CE=BD,在Rt△DCE中运用勾股定理就可求出DE.
解:(1)∵△ABC和△ADE都是等腰Rt△,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAD=∠CAE.
在△ACE和△ABD中,
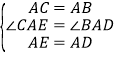 ,
,
∴△ACE≌△ABD;
(2)∵△ACE≌△ABD,
∴∠ACE=∠ABD=45°,
∴∠BCE=∠BCA+∠ACE=45°+45°=90°;
∴∠BCE的度数不变,为90°;
(3)①点D在线段BC上时,如图1,
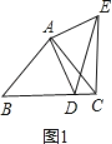
∵AB=AC=![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=4.
∵CD=1,
∴BD=3.
∵△ACE≌△ABD,
∴CE=BD=3.
∵∠BCE=90°,
∴DE=![]() =
=![]() =
=![]() ;
;
②点D在线段BC延长线上时,如图2,
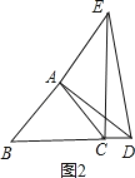
∵AB=AC=![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=4.
∵CD=1,
∴BD=5.
∵△ACE≌△ABD,
∴CE=BD=5.
∵∠BCE=90°,
∴∠ECD=90°,
∴DE=![]() =
=![]() =
=![]() .
.
综上所述:DE的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,求两次摸出的小球的标号之和大于4的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt
 中,∠A=90°,点O在AC上,⊙O切BC于点E,A在⊙O上,若AB=5,AC=12,求⊙O的半径.
中,∠A=90°,点O在AC上,⊙O切BC于点E,A在⊙O上,若AB=5,AC=12,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某长途客运公司规定每位旅客可以免费托运一定重量的行李,超过部分则需缴交行李托运费.行李费托运费y(元)与行李重量x(千克)之间的函数关系如图所示.
(1)求y与x的函数关系式;
(2)每位旅客最多可以免费托运多少千克行李?
(3)某旅客行托运行李100千克,应交多少行李托运费?

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图:若
 ,点
,点 在
在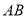 、
、 内部,则
内部,则 、
、 、
、 之间有何数量关系?请证明你的结论.
之间有何数量关系?请证明你的结论.
(2)如图,若
 ,将点
,将点 移到
移到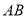 、
、 外部,则
外部,则 、
、 、
、 的数量关系是______.
的数量关系是______.
(3)在下图中,将直线
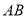 绕点
绕点 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线 于点
于点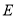 ,则
,则 、
、 、
、 、
、 之间满足的数量关系是______.
之间满足的数量关系是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 y=x2+bx+c与x
y=x2+bx+c与x 轴交于A(-2,0),B(6,0)两点.
轴交于A(-2,0),B(6,0)两点.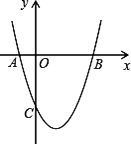
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)点P为y轴右侧抛物线上一个动点,若S△PAB=32,求出此时P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AC,点D为AC的中点,B是直线AC上的一点,且 BC=
 AB,BD=1cm,则线段AC的长为( )
AB,BD=1cm,则线段AC的长为( )A.
 B.
B.  C.
C.  或
或 D.
D.  或
或
相关试题

