【题目】如图,在Rt ![]() 中,∠A=90°,点O在AC上,⊙O切BC于点E,A在⊙O上,若AB=5,AC=12,求⊙O的半径.
中,∠A=90°,点O在AC上,⊙O切BC于点E,A在⊙O上,若AB=5,AC=12,求⊙O的半径.
参考答案:
【答案】解:连接BO、EO,设⊙O半径为 ![]() ,
,
在Rt△ABC![]() 中,根据勾股定理,有:
中,根据勾股定理,有: ![]()
∵ ![]() ,∴
,∴ ![]()
即 ![]()
解得 ![]() .
.![]() 的半径长为
的半径长为 ![]()
【解析】连接BO、EO,设⊙O半径为 x ,在Rt△ABC 中,根据勾股定理可求出BC的长,根据△ABC的面积=△ABO的面积+△BCO的面积得到关于x的方程,解方程可求出半径.
【考点精析】通过灵活运用勾股定理的概念和切线的性质定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用长为1cm,2 cm,3 cm的三条线段围成三角形的事件是:( )
A.随机事件
B.必然事件
C.不可能事件
D.以上说法都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,求两次摸出的小球的标号之和大于4的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某长途客运公司规定每位旅客可以免费托运一定重量的行李,超过部分则需缴交行李托运费.行李费托运费y(元)与行李重量x(千克)之间的函数关系如图所示.
(1)求y与x的函数关系式;
(2)每位旅客最多可以免费托运多少千克行李?
(3)某旅客行托运行李100千克,应交多少行李托运费?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已等腰Rt△ABC中,∠BAC=90°.点D从点B出发沿射线BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.
(1)如图,求证:△ACE≌△ABD;
(2)点D运动时,∠BCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3)若AC=
 ,当CD=1时,请直接写出DE的长.
,当CD=1时,请直接写出DE的长.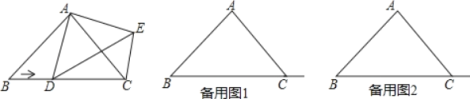
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图:若
 ,点
,点 在
在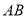 、
、 内部,则
内部,则 、
、 、
、 之间有何数量关系?请证明你的结论.
之间有何数量关系?请证明你的结论.
(2)如图,若
 ,将点
,将点 移到
移到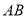 、
、 外部,则
外部,则 、
、 、
、 的数量关系是______.
的数量关系是______.
(3)在下图中,将直线
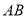 绕点
绕点 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线 于点
于点 ,则
,则 、
、 、
、 、
、 之间满足的数量关系是______.
之间满足的数量关系是______.
相关试题

