搜索
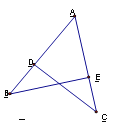
【题目】如图：ΔABE≌ΔACD，AB=10cm，∠A=60°，∠B=30°，则AD=_____ cm，∠ADC=_____。
参考答案：
【答案】5，90°
【解析】试题分析：此题主要考查了全等三角形的性质，以及三角形内角和定理和直角三角形的性质，关键是掌握全等三角形的对应边相等，全等三角形的对应角相等．首先根据全等三角形的性质可得∠C=∠B=30°，AC=AB=10cm，再根据三角形内角和计算出∠ADC的度数，再根据直角三角形的性质可得AD=
AC=5cm．
解：∵△ABE≌△ACD，
∴∠C=∠B=30°，AC=AB=10cm，
∵∠A=60°，
∴∠ADC=180°-60°-30°=90°，
∴AD=
AC=5cm，
故答案为：5，90°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(2016山东省聊城市第29题)(1)、已知：△ABC是等腰三角形，其底边是BC，点D在线段AB上，E是直线BC上一点，且∠DEC=∠DCE，若∠A=60°（如图①）．求证：EB=AD；
(2)、若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其它条件不变（如图②），（1）的结论是否成立，并说明理由；
(3)、若将（1）中的“若∠A=60°”改为“若∠A=90°”，其它条件不变，则
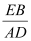的值是多少？（直接写出结论，不要求写解答过程）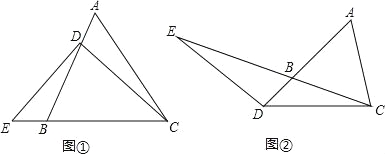 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线a、b、c表示三条公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有_______处.
-
科目： 来源： 题型：
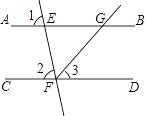
查看答案和解析>>【题目】如图，已知直线AB、CD被直线EF所截，FG平分∠EFD，∠1=∠2=80°，求∠BGF的度数．
解：因为∠1=∠2=80°（已知），
所以AB∥CD__________
所以∠BGF+∠3=180°__________
因为∠2+∠EFD=180°（邻补角的性质）．
所以∠EFD=________．（等式性质）．
因为FG平分∠EFD（已知）．
所以∠3=________∠EFD（角平分线的性质）．
所以∠3=________．（等式性质）．
所以∠BGF=________．（等式性质）．
-
科目： 来源： 题型：
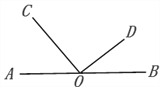
查看答案和解析>>【题目】如图，O是直线AB上的一点，OC⊥OD，垂足为O.
（1）若∠BOD=32°，求∠AOC的度数；
（2）若∠AOC：∠BOD=2:1，直接写出∠BOD的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市元宵节灯展参观人数约为470000，将这个数用科学记数法表示为（ ）
A. 4.7×106 B. 4.7×105 C. 0.47×106 D. 47×104
-
科目： 来源： 题型：
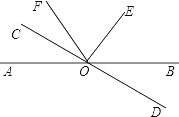
查看答案和解析>>【题目】如图，已知直线AB和CD相交于O点，∠COE=90°，OF平分∠AOE，∠COF=28°，求∠BOD的度数．
相关试题
