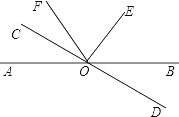
【题目】如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数.
参考答案:
【答案】34°
【解析】试题分析:根据角的和差关系可得∠EOF的度数,根据角平分线的定义可得∠AOF的度数,再根据角的和差关系求得∠AOC,根据∠BOD和∠AOC是对顶角,可求得∠BOD的度数.
试题解析:由角的和差关系可得:∠EOF=∠COE﹣∠COF=90°﹣28°=62°,
由角平分线的定义可得:∠AOF=∠EOF=62°,
由角的和差关系可得:∠AOC=∠AOF﹣∠COF=62°﹣28°=34°,
由对顶角相等性质可得∠BOD=∠AOC=34°.
点睛:本题主要考查角的和差关系的计算,角平分线的定义和对顶角的性质,解决本题关键是要熟练掌握角平分线的定义,能够分析简单的几何图形,利用角的和差关系进行说理计算.
-
科目: 来源: 题型:
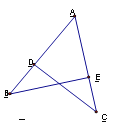
查看答案和解析>>【题目】如图:ΔABE≌ΔACD,AB=10cm,∠A=60°,∠B=30°,则AD=_____ cm,∠ADC=_____。
-
科目: 来源: 题型:
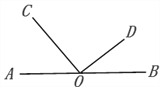
查看答案和解析>>【题目】如图,O是直线AB上的一点,OC⊥OD,垂足为O.
(1)若∠BOD=32°,求∠AOC的度数;
(2)若∠AOC:∠BOD=2:1,直接写出∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市元宵节灯展参观人数约为470000,将这个数用科学记数法表示为( )
A. 4.7×106 B. 4.7×105 C. 0.47×106 D. 47×104
-
科目: 来源: 题型:
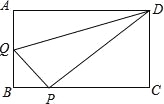
查看答案和解析>>【题目】(2016宁夏第26题)在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4x=_____.
相关试题

