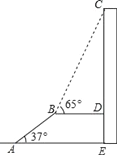
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
参考答案:
【答案】大楼CE的高度是27m.
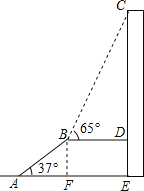
【解析】试题分析:作BF⊥AE于点F.则BF=DE,在直角△ABF中利用三角函数求得BF的长,在直角△CDB中利用三角函数求得CD的长,则CE即可求得.
试题解析:过点B作BF⊥AE于点F.则BF=DE.
在Rt△ABF中,sin∠BAF=![]() ∴BF=ABsin∠BAF=10×
∴BF=ABsin∠BAF=10×![]() =6(m).
=6(m).
又在Rt△CDB中,tan∠CBD=![]() ,∴CD=BDtan65°=10×
,∴CD=BDtan65°=10×![]() ≈21(m)
≈21(m)
∴CE=DE+CD=BF+CD=6+21=27(m).
答:大楼CE的高度是27m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测倾器测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.则河的宽度为________米(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90,CD⊥AB,BC=1.
(1)如果∠BCD=30,求AC;
(2)如果tan∠BCD=
 ,求CD.
,求CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F是平行四边形ABCD对角线AC上两点,AE=CF.
证明(1)△ABE≌△CDF;
(2)BE∥DF.

-
科目: 来源: 题型:
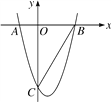
查看答案和解析>>【题目】如图,已知抛物线y=x2-x-6与x轴交于点A和B,点A在点B的左边,与y轴的交点为C.
(1)用配方法求该抛物线的顶点坐标;
(2)求sin∠OCB的值;
(3)若点P(m,m)在该抛物线上,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

相关试题

