搜索
【题目】在综合实践课上，小聪所在小组要测量一条河的宽度，如图，河岸EF∥MN，小聪在河岸MN上点A处用测倾器测得河对岸小树C位于东北方向，然后沿河岸走了30米，到达B处，测得河对岸电线杆D位于北偏东30°方向，此时，其他同学测得CD＝10米．则河的宽度为________米(结果保留根号).
参考答案：
【答案】
(或
)
【解析】试题分析：如图作BH⊥EF，CK⊥MN，垂足分别为H、K，则四边形BHCK是矩形，
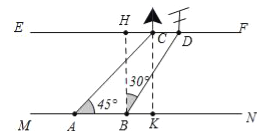
设CK=HB=x，
∵∠CKA=90°，∠CAK=45°，
∴∠CAK=∠ACK=45°，
∴AK=CK=x，BK=HC=AK﹣AB=x﹣30，
∴HD=x﹣30+10=x﹣20，
在RT△BHD中，∵∠BHD=30°，∠HBD=30°，
∴tan30°=
，
解得x=30+10
．
∴河的宽度为（30+10）米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一只蚂蚁由(0，0)先向上爬4个单位长度，再向右爬3个单位长度，再向下爬2个单位长度后，它所在位置的坐标是____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若使等式(－4)□(－6)＝2成立，则□中应填入的运算符号是( )
A. ＋ B. － C. × D. ÷
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B．
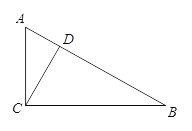
（1）求证：CD⊥AB；
（2）在（1）中画△ABC的角平分线AE，交CD于点F，试判断∠AEC与∠CFE的数量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．
（1）求证：∠ACD=∠B；
（2）如图2，∠BDC的平分线分别交AC，BC于点E，F；
①求tan∠CFE的值；
②若AC=3，BC=4，求CE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】规定两数a，b之间的一种运算，记作(a，b)：如果
，那么(a，b)=c．例如：因为23=8，所以(2，8)=3．
（1）根据上述规定，填空：
（3，27）=_______，（5，1）=_______，（2，
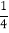
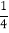）=_______．（2）小明在研究这种运算时发现一个现象：（3n，4n）=（3，4）小明给出了如下的证明：
设（3n，4n）=x，则（3n）x=4n，即（3x）n=4n
所以3x=4，即（3，4）=x，
所以（3n，4n）=（3，4）．
请你尝试运用这种方法证明下面这个等式：(3，4)+(3，5)=(3，20)
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：关于
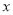的一元二次方程
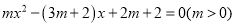，（1）求证：方程有两个不相等的实数根且其中一个根为定值。
（2）设方程的两个实数根分别为
， 
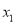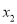(其中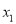
<
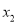)。若y是关于m的函数，且
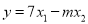，求这个函数的解析式；并求当自变量
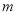的取值范围满足什么条件时， 
。
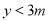相关试题
