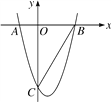
【题目】如图,已知抛物线y=x2-x-6与x轴交于点A和B,点A在点B的左边,与y轴的交点为C.
(1)用配方法求该抛物线的顶点坐标;
(2)求sin∠OCB的值;
(3)若点P(m,m)在该抛物线上,求m的值.
参考答案:
【答案】(1)抛物线的顶点坐标为![]() ;(2) sin∠OCB=
;(2) sin∠OCB=![]() ;(3) m1=1+
;(3) m1=1+![]() ,m2=1-
,m2=1-![]() .
.
【解析】(1)根据配方法,可得顶点式解析式,根据顶点式解析式,可得抛物线的顶点;
(2)根据函数值为0,可得B点坐标,根据自变量为0,可得C点坐标,根据勾股定理,可得BC的长,根据正弦的意义,可得答案;
(3)根据图象上的点的坐标满足函数解析式,可得一元二次方程,根据解一元二次方程,可得答案.
解:(1)∵y=x2x6=x2x+![]()
![]() 6=(x
6=(x![]() )2
)2![]() ,
,
∴抛物线的顶点坐标为(![]() ,
,![]() );
);
(2)令x2x6=0,
解得x1=2,x2=3,
∴点B的坐标为(3,0),
又点C的坐标为(0,6),
∴BC=![]() ,
,
∴sin∠OCB=![]() ;
;
(3)∵点P(m,m)在这个二次函数的图象上,
∴m2m6=m,
即m22m6=0,
解得m1=1+![]() ,m2=1-
,m2=1-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90,CD⊥AB,BC=1.
(1)如果∠BCD=30,求AC;
(2)如果tan∠BCD=
 ,求CD.
,求CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F是平行四边形ABCD对角线AC上两点,AE=CF.
证明(1)△ABE≌△CDF;
(2)BE∥DF.

-
科目: 来源: 题型:
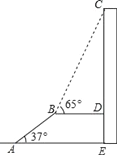
查看答案和解析>>【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈
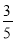 ,tan37°≈
,tan37°≈ ,sin65°≈
,sin65°≈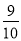 ,tan65°≈
,tan65°≈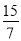 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
相关试题

