【题目】在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连接BD,CD,其中CD交直线AP于点E. 
(1)依题意补全图1;
(2)若∠PAB=30°,求∠ACE的度数;
(3)如图2,若60°<∠PAB<120°,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并证明. 
参考答案:
【答案】
(1)解:所作图形如图1所示:

(2)解:连接AD,如图1.
∵点D与点B关于直线AP对称,
∴AD=AB,∠DAP=∠BAP=30°,
∵AB=AC,∠BAC=60°,
∴AD=AC,∠DAC=120°,
∴2∠ACE+60°+60°=180°,
∴∠ACE=30°

(3)解:线段AB,CE,ED可以构成一个含有60°角的三角形.
证明:连接AD,EB,如图2.
∵点D与点B关于直线AP对称,
∴AD=AB,DE=BE,
∴∠EDA=∠EBA,
∵AB=AC,AB=AD,
∴AD=AC,
∴∠ADE=∠ACE,
∴∠ABE=∠ACE.
设AC,BE交于点F,
又∵∠AFB=∠CFE,
∴∠BAC=∠BEC=60°,
∴线段AB,CE,ED可以构成一个含有60°角的三角形.

【解析】(1)根据题意作出图形;(2)根据题意可得∠DAP=∠BAP=30°,然后根据AB=AC,∠BAC=60°,得出AD=AC,∠DAC=120°,最后根据三角形的内角和公式求解;(3)由线段AB,CE,ED可以构成一个含有60度角的三角形,连接AD,EB,根据对称可得∠EDA=∠EBA,然后证得AD=AC,最后即可得出∠BAC=∠BEC=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6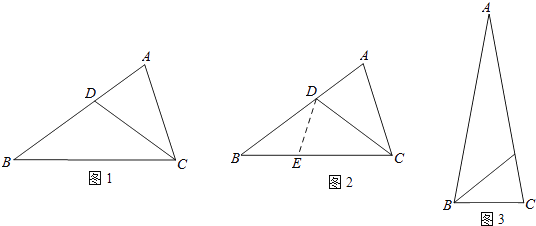
求BC的长.
小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).
请回答:
(1)△BDE是三角形.
(2)BC的长为 .
参考小聪思考问题的方法,解决问题:
如图3,已知△ABC中,AB=AC,∠A=20°,BD平分∠ABC,BD=2.3,BC=2.求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为3,圆心O到直线l的距离为3,直线l与⊙O的位置关系是( )
A. 相交B. 相切C. 相离D. 相交或相切
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,∠A﹦100°,则∠B=_________。
-
科目: 来源: 题型:
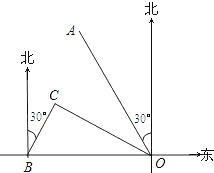
查看答案和解析>>【题目】如图,港口B位于港口O正西方向120海里处,小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏西30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去.
(1)快艇从港口B到小岛C需要多少时间?
(2)快艇从小岛C出发后最少需要多少时间才能和考察船相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 相等的圆心角所对的弧相等B. 三角形的内心到三角形三个顶点距离相等
C. 等弧所对的弦相等D. 圆的切线垂直于半径
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A. 过弦的中点的直线平分弦所对的弧;
B. 过弦的中点的直线必经过圆心;
C. 弦所对的两条弧的中点的连线垂直平分弦,且过圆心;
D. 弦的垂线平分弦所对的弧。
相关试题

