【题目】阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{﹣1,2,3}=![]() =
=![]() ;min{﹣1,2,3}=﹣1;min{﹣1,2,a}=
;min{﹣1,2,3}=﹣1;min{﹣1,2,a}=![]()
解决下列问题:
(1)若min{2,2x+2,4﹣2x}=2,则x的范围__________;
(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x;
②根据①,你发现了结论“如果M{a,b,c}=min{a,b,c},那么__________(填a,b,c的大小关系)”.
③运用②的结论,若M{2x+y+2,x+2y,2x﹣y}=min{2x+y+2,x+2y,2x﹣y},求x+y的值.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;③-4
;③-4
【解析】
(1)因为用min(a,b,c)表示这三个数中最小的数,由min{2,2x+2,42x}=2,得出2x+2≥2,且42x≥2,两个式子同时成立,据此即可求得x的范围;
(2)①M{2,x+1,2x}=![]() =x+1,若M{2,x+1,2x}=min{2,x+1,2x},则x+1是2、x+1、2x中最小的一个,即:x+1≤2且x+1≤2x,据此即可求得x的值;
=x+1,若M{2,x+1,2x}=min{2,x+1,2x},则x+1是2、x+1、2x中最小的一个,即:x+1≤2且x+1≤2x,据此即可求得x的值;
②根据①可以得到结论:当三个数的平均数等于三个数中的最小的数,则这几个数相等,据此即可写出;
③根据结论,三个数相等,即可求得x,y的值,从而求得x+y的值;
(1)由min{2,2x+2,42x}=2,得![]() ,即0≤x≤1,
,即0≤x≤1,
故答案为:0≤x≤1;
(2)①∵M{2,x+1,2x}=min{2,x+1,2x},
∴![]() ,解得:
,解得:![]() ,
,
∴x=1;
②证明:由M{a,b,c}=min{a,b,c},可令![]() =a,即b+c=2a;
=a,即b+c=2a;
又∵ ,
,
解之得:a+c≤2b,a+b≤2c;
把b+c=2a代入a+c≤2b 可得c≤b;
把b+c=2a代入a+b≤2c可得b≤c;
∴b=c;将b=c代入b+c=2a得c=a;
∴a=b=c,
故答案为:a=b=c;
③由②可得![]()
解之得y=1,x=3,
∴x+y=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C. 若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为
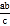
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车
B型客车
载客量(人/辆)
40
25
日租金(元/辆)
320
200
车辆数(辆)
a
b
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.

(1)如图2,若四边形ABCD为“可分四边形”,∠DAB为“可分角”,且∠DCB=∠DAB,则∠DAB=°.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A,B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).

(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,点E、F分别是AD、AB的中点,EF交AC于点G,那么AG:GC的值为( )

A.1:2
B.1:3
C.1:4
D.2:3 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x,y的二元一次方程组
 的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求m的值.
的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求m的值.
相关试题

