【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O交AB于点D,线段BC上有一点P.
(1)当点P在什么位置时,直线DP与⊙O有且只有一个公共点,补全图形并说明理由.
(2)在(1)的条件下,当BP=![]() ,AD=3时,求⊙O半径.
,AD=3时,求⊙O半径.
参考答案:
【答案】(1)补图见解析;理由见解析;(2)![]() .
.
【解析】
(1)根据题意补全图形如图所示,情况一:点P在过点D与OD垂直的直线与BC的交点处,根据切线的定义即可得到结论;情况二:如图,当点P是BC的中点时,直线DP与⊙O有且只有一个公共点,连接CD,OD,根据圆周角定理得到∠ADC=∠BDC=90°,根据直角三角形的性质得到DP=CP,根据切线的判定定理即可得到结论;
(2)由题意可知在Rt△BCD中,根据直角三角形的性质得到BC=2BP,求得BC=![]() ,根据相似三角形的性质和勾股定理即可得到结论.
,根据相似三角形的性质和勾股定理即可得到结论.
解:(1)补全图形如图所示,
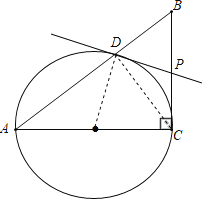
情况一:点P在过点D与OD垂直的直线与BC的交点处,
理由:经过半径外端,并且垂直于这条半径的直线是圆的切线;
情况二:如图,当点P是BC的中点时,直线DP与⊙O有且只有一个公共点,
证明:连接CD,OD,如上图,
∵AC是⊙O的直径,
∴∠ADC=∠BDC=90°,
∵点P是BC的中点,
∴DP=CP,
∴∠PDC=∠PCD,
∵∠ACB=90°,
∴∠PCD+∠DCO=90°,
∵OD=OC,
∴∠DCO=∠ODC,
∴∠PDC+∠ODC=90°,
∴∠ODP=90°,
∴DP⊥OD,
∴直线DP与⊙O相切;
(2)在Rt△BCD中,∵∠BDC=90°,P是BC的中点,
∴BC=2BP,
∵BP=![]() ,
,
∴BC=![]() ,
,
∵∠ACB=∠BDC=90°,∠B=∠B,
∴△ACB∽△CDB,
∴![]() ,
,
∴![]() ,
,
设AB=x,
∵AD=3,
∴BD=x﹣3,
∴x(x﹣3)=(![]() )2,
)2,
∴x=5(负值舍去),
∴AB=5,
∵∠BDC=90°,
∴AC=![]() =
=![]() ,
,
∴OC=![]() AC=
AC=![]() ,
,
即⊙O的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,反比例函数y=
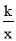 的图象与一次函数y=2x﹣1的图象交于A、B两点,已知A(m,﹣3).
的图象与一次函数y=2x﹣1的图象交于A、B两点,已知A(m,﹣3).(1)求k及点B的坐标;
(2)若点C是y轴上一点,且S△ABC=5,直接写出点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息:

a.截止3月1日20时,全国已有11个省份工业企业复工率在90%以上,主要位于东南沿海地区,位居前三的分别是贵州(100%)、浙江(99.8%)、江苏(99%).
b.各省份复工率数据的频数分布直方图如图1(数据分成6组,分别是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c.如图2,在b的基础上,画出扇形统计图:
d.截止到2020年3月1日各省份的复工率在80<x≤90这一组的数据是:
81.3
83.9
84
87.6
89.4
90
90
e.截止到2020年3月1日各省份的复工率的平均数、中位数、众数如下:
日期
平均数
中位数
众数
截止到2020年3月1日
80.79
m
50,90
请解答以下问题:
(1)依据题意,补全频数分布直方图;
(2)扇形统计图中50<x≤60这组的圆心角度数是 度(精确到0.1).
(3)中位数m的值是 .
(4)根据以上统计图表简述国内企业截止3月1日的复工率分布特征.
-
科目: 来源: 题型:
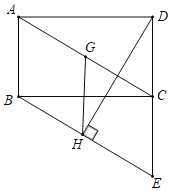
查看答案和解析>>【题目】如图,矩形ABCD,过点B作BE∥AC交DC的延长线于点E.过点D作DH⊥BE于H,G为AC中点,连接GH.
(1)求证:BE=AC.
(2)判断GH与BE的数量关系并证明.
-
科目: 来源: 题型:
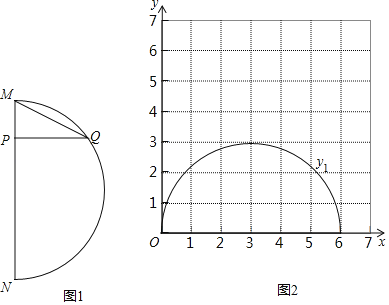
查看答案和解析>>【题目】如图1,在弧MN和弦MN所组成的图形中,P是弦MN上一动点,过点P作弦MN的垂线,交弧MN于点Q,连接MQ.已知MN=6cm,设M、P两点间的距离为xcm,P、Q两点间的距离为y1cm,M、Q两点间的距离为y2cm.小轩根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小轩的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:x/cm.
x/cm
0
1
2
3
4
5
6
y1/cm
0
2.24
2.83
3.00
2.83
2.24
0
y2/cm
0
2.45
3.46
4.24
m
5.48
6
上表中m的值为 .(保留两位小数)
(2)在同一平面直角坐标系xOy(图2)中,函数y1的图象如图,请你描出补全后的表中y2各组数值所对应的点(x,y2),并画出函数y2的图象;
(3)结合函数图象,解决问题:当△MPQ有一个角是30°时,MP的长度约为 cm.(保留两位小数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知抛物线y=ax2+bx﹣1交y轴于点P.
(1)过点P作与x轴平行的直线,交抛物线于点Q,PQ=4,求
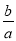 的值;
的值;(2)横纵坐标都是整数的点叫做整点.在(1)的条件下,记抛物线与x轴所围成的封闭区域(不含边界)为W.若区域W内恰有4个整点,结合函数图象,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,点M为BC中点.点P为AB边上一动点,点D为BC边上一动点,连接DP,以点P为旋转中心,将线段PD逆时针旋转90°,得到线段PE,连接EC.
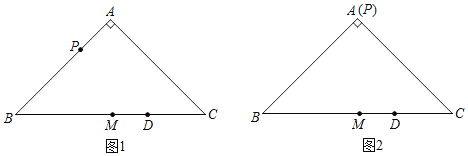
(1)当点P与点A重合时,如图2.
①根据题意在图2中完成作图;
②判断EC与BC的位置关系并证明.
(2)连接EM,写出一个BP的值,使得对于任意的点D总有EM=EC,并证明.
相关试题

