【题目】(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.

参考答案:
【答案】(1)BD =CE,理由见解析;(2)BD长是![]() cm; (3) BD长是(
cm; (3) BD长是(![]() -3)cm.
-3)cm.
【解析】试题分析:(1)证明△EAC与△BAD全等即可得证;
(2)连接EC、EB,通过证明△EAC与△BAD 全等,得到BD=CE.由勾股定理可得EC的长,从而可得BD长;
(3)如图,在线段AC的右侧过点A作AE⊥AB于A,交BC的延长线于点E,通过证明△EAC与△BAD全等,从而得BD=CE,从而求得BD长.
试题解析:(1)BD =CE.
理由:∵△ABE和△ACD都是等边三角形,∴∠BAE=∠CAD=60°,AE=AB,AC=AD,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD, ∴△EAC≌△BAD (SAS) ,∴BD=CE.
(2)如图,连接EC、EB.
在正方形ABNE和正方形ACMD中
∵![]() ,AE=AB ,∠BAE=
,AE=AB ,∠BAE=![]() ,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD (SAS) ,∴BD=CE.
,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD (SAS) ,∴BD=CE.
∵AE=AB=5,∴BE=![]() , ∠ABE=∠AEB=45.
, ∠ABE=∠AEB=45.
又∵∠ABC=45,∴∠ABC+∠ABE=45+45=90, ∴EC=![]() =
=![]() =
=![]() ,
,
∴BD=CE=![]() (cm).
(cm).
答:BD长是![]() cm.
cm.

(3)如图,在线段AC的右侧过点A作AE⊥AB于A,交BC的延长线于点E,
∴∠BAE=90,
又∵∠ABC=45,∴∠E=∠ABC=45,∴AE=AB=5,BE=![]() =
=![]() .
.
又∵∠ACD=∠ADC=45 ,∴∠BAE= ∠DAC=90, ∴∠BAE![]() ∠BAC=∠DAC
∠BAC=∠DAC![]() ∠BAC,
∠BAC,
即∠EAC=∠BAD,∴△EAC≌△BAD (SAS) , ∴BD=CE.
∵BC=3,∴BD=CE=(![]() -3)(cm).
-3)(cm).
答:BD长是(![]() -3)cm.
-3)cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:
 ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)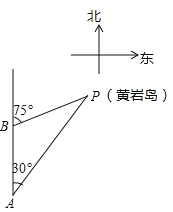
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在抄分解因式的题目时,不小心漏抄了x的指数,他只知道该数为不大于10的正整数,并且能利用平方差公式分解因式,他抄在作业本上的式子是x□﹣4y2(“□”表示漏抄的指数),则这个指数可能的结果共有( )
A. 2种 B. 3种 C. 4种 D. 5种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将ABCD的边BA延长到点E,使AE=AB,连接EC,交AD于点F,连接AC、ED.
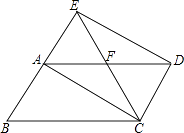
(1)求证:四边形ACDE是平行四边形;
(2)若∠AFC=2∠B,求证:四边形ACDE是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有一列式子:①552-452;②5552-4452;③55552-44452…则第⑧个式子的计算结果用科学记数法可表示为( )
A. 1.1111111×1016 B. 1.1111111×1027
C. 1.111111×1056 D. 1.1111111×1017
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
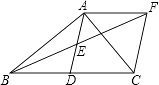
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】将代数式3x2y+5xy2﹣3y3﹣5x3按y的降幂排列是( )
A.﹣5x3+3x2y+5xy2﹣3y3
B.﹣3y3+5xy2+3x2y﹣5x3
C.﹣5x3﹣3y3+3x2y+5xy2
D.3x2y+5xy2﹣3y3﹣5x3
相关试题

