【题目】如图,射线AB∥射线CD,∠CAB与∠ACD的平分线交于点E,AC=4,点P是射线AB上的一动点,连结PE并延长交射线CD于点Q.给出下列结论:①△ACE是直角三角形;②S四边形APQC=2S△ACE;③设AP=x,CQ=y,则y关于x的函数表达式是y=﹣x+4(0≤x≤4),其中正确的是( )

A. ①②③B. ①②C. ①③D. ②③
参考答案:
【答案】A
【解析】
①正确.由AB∥CD,推出∠BAC+∠DCA=180°,由∠ACE=![]() ∠DCA,∠CAE=
∠DCA,∠CAE=![]() ∠BAC,即可推出∠ACE+∠CAE=
∠BAC,即可推出∠ACE+∠CAE=![]() (∠DCA+∠BAC)=90°,延长即可解决问题;
(∠DCA+∠BAC)=90°,延长即可解决问题;
②正确.首先证明AC=AK,再证明△QCE≌△PKE,即可解决问题;
③正确.只要证明AP+CQ=AC即可解决问题.
解:如图延长CE交AB于K.
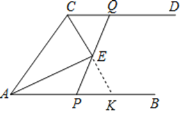
∵AB∥CD,
∴∠BAC+∠DCA=180°,
∵∠ACE=![]() ∠DCA,∠CAE=
∠DCA,∠CAE=![]() ∠BAC,
∠BAC,
∴∠ACE+∠CAE=![]() (∠DCA+∠BAC)=90°,
(∠DCA+∠BAC)=90°,
∴∠AEC=90°,
∴AE⊥CK,△AEC是直角三角形,故①正确,
∵∠QCK=∠AKC=∠ACK,
∴AC=AK,
∵AE⊥CK,
∴CE=EK,
在△QCE和△PKE中,
 ,
,
∴△QCE≌△PKE,
∴CQ=PK,S△QCE=S△PEK,
∴S四边形APQC=S△ACK=2S△ACE,故②正确,
∵AP=x,CQ=y,AC=4,
∴AP+CQ=AP+PK=AK=AC,
∴x+y=4,
∴y=-x+4(0≤x≤4),故③正确,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2﹣10x+16=0的两个根,且抛物线的对称轴是直线x=﹣2.

(1)求A,B,C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC,BC,若点E是线段AB上的一个动点(与点A,点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和直尺画图:
(1)补全△A′B′C′;
(2)作出△ABC的中线CD;
(3)画出BC边上的高线AE;
(4)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有 个.(注:格点指网格线的交点)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A.3sin40°
B.3sin50°
C.3tan40°
D.3tan50° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )
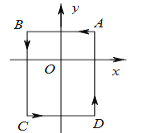
A. (-1,0)B. (1,2)C. (1,-1)D. (0,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A、B、C三点的坐标分别为(﹣6,7)、(﹣3,0)、(0,3).
(1)画出△ABC,并求△ABC的面积;
(2)在△ABC中,点C经过平移后的对应点为C′(5,4),将△ABC作同样的平移得到△A′B′C′, 画出平移后的△A′B′C′,并写出点A′,B′的坐标;
(3)已知点P(﹣3,m)为△ABC内一点,将点P向右平移4个单位后,再向下平移6个单位得到点Q(n,﹣3),则m= ,n= .

相关试题

