【题目】如图,点P是反比例函数y= ![]() (k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=
(k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= ![]() .
.
(1)k的值是;
(2)若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是 .
参考答案:
【答案】
(1)-4
(2)0<a<2或 ![]() <a<
<a< ![]()
【解析】解:(1.)如图,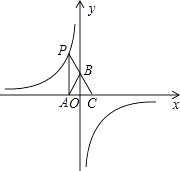
PA垂直x轴于点A(﹣1,0),
∴OA=1,可设P(﹣1,t).
又∵AB= ![]() ,
,
∴OB= ![]() =
= ![]() =2,
=2,
∴B(0,2).
又∵点C的坐标为(1,0),
∴直线BC的解析式是:y=﹣2x+2.
∵点P在直线BC上,
∴t=2+2=4
∴点P的坐标是(﹣1,4),
∴k=﹣4.
所以答案是:﹣4;
解法二:用相似三角形
由题意易得△CPA~CBO,
∴ ![]()
∴ ![]()
∴AP=4,
∴k=﹣4.
(2.)分类讨论
①如图1,延长线段BC交双曲线于点M.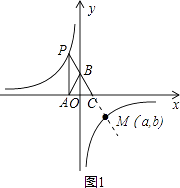
由(1)知,直线BC的解析式是y=﹣2x+2,反比例函数的解析式是y=﹣ ![]() .
.
则 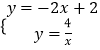 ,
,
解得, ![]() 或
或 ![]() (不合题意,舍去).
(不合题意,舍去).
根据图示知,当0<a<2时,∠MBA<∠ABC;
②如图,作C关于直线AB的对称点C′,连接BC′并延长交双曲线于点M′.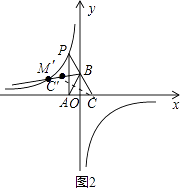
∵A(﹣1,0),B(0,2),
∴直线AB的解析式为:y=2x+2.
直线CC′是与直线AB垂直的,
根据两条直线垂直,两直线的斜率互为负倒数,即:k1k2=﹣1
可设CC′解析式为:y=﹣ ![]() x+b,
x+b,
∵C(1,0),
∴b= ![]() ,
,
∴CC′解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
∵AC=AC′=2,
∴设C′点横坐标为:x,则纵坐标为:﹣ ![]() x+
x+ ![]() ,
,
∴(﹣x﹣AO)2+(﹣ ![]() x+
x+ ![]() )2=(AC′)2 ,
)2=(AC′)2 ,
解得:x1=﹣ ![]() ,x2=1(不合题意舍去),
,x2=1(不合题意舍去),
∴C′(﹣ ![]() ,
, ![]() ),则易求直线BC′的解析式为:y=
),则易求直线BC′的解析式为:y= ![]() x+2,
x+2,
∴ 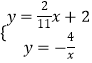 ,
,
解得:x1= ![]() ,x2=
,x2= ![]() ,
,
则根据图示知,当 ![]() <a<
<a< ![]() 时,∠MBA<∠ABC.
时,∠MBA<∠ABC.
综合①②知,当0<a<2或 ![]() <a<
<a< ![]() 时,∠MBA<∠ABC.
时,∠MBA<∠ABC.
故答案是:0<a<2或 ![]() <a<
<a< ![]() .
.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )

A.AF=AE
B.△ABE≌△AGF
C.EF=2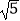
D.AF=EF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(﹣4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.

(1)求直线AB的函数解析式;
(2)当点P在线段AB(不包括A,B两点)上时.
①求证:∠BDE=∠ADP;
②设DE=x,DF=y.请求出y关于x的函数解析式;
(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,则
 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12 m.设AD的长为x m,DC的长为y m.

(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.

(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论: ①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )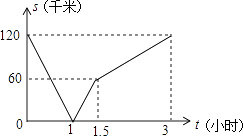
A.4
B.3
C.2
D.1
相关试题

