【题目】△ABC中,AB=13cm,AC=15cm,高AD=12,则BC的长为( )
A.14
B.4
C.14或4
D.以上都不对
参考答案:
【答案】C
【解析】解:(1)如图,锐角△ABC中,AB=13,AC=15,BC边上高AD=12,
在Rt△ABD中AB=13,AD=12,由勾股定理得
BD2=AB2﹣AD2=132﹣122=25,
则BD=5,
在Rt△ABD中AC=15,AD=12,由勾股定理得
CD2=AC2﹣AD2=152﹣122=81,
则CD=9,
故BC=BD+DC=9+5=14;
2)钝角△ABC中,AB=13,AC=15,BC边上高AD=12,
在Rt△ABD中AB=13,AD=12,由勾股定理得
BD2=AB2﹣AD2=132﹣122=25,
则BD=5,
在Rt△ACD中AC=15,AD=12,由勾股定理得
CD2=AC2﹣AD2=152﹣122=81,
则CD=9,
故BC的长为DC﹣BD=9﹣5=4.
故选:C.

【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB=20,C是AB上的一点,D为CB上的一点,E为DB的中点,DE=3.
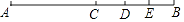
(1)若CE=8,求AC的长;
(2)若C是AB的中点,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知A(0,a),B(b,0),且a、b满足a2﹣4a+20=8b﹣b2 .
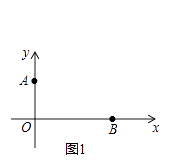
(1)求A、B两点的坐标;
(2)如图2,连接AB,若D(0,﹣6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论;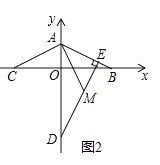
(3)如图3,在(2)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由.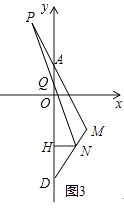
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为2的⊙O中,弦AB=2,⊙O上存在点C,使得弦AC=2
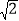 ,则∠BOC=____°.
,则∠BOC=____°.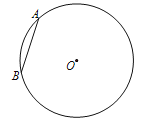
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2-2m x+m2+m+1的图像与x轴交于A、B两点,点C为顶点.
(1)求m的取值范围;
(2)若将二次函数的图像关于x轴翻折,所得图像的顶点为D,若CD=8.求四边形ACBD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】用作位似形的方法,可以将一个图形放大或缩小,位似中心( )
A.只能选在原图形的外部
B.只能选在原图形的内部
C.只能选在原图形的边上
D.可以选择任意位置 -
科目: 来源: 题型:
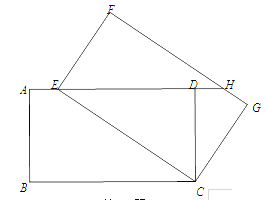
查看答案和解析>>【题目】如图,将矩形ABCD绕点C旋转得到矩形FECG,点E在AD上,延长ED交FG于点H.
(1)求证:△EDC≌△HFE;
(2)连接BE、CH.
①四边形BEHC是怎样的特殊四边形?证明你的结论.
②当AB与BC的比值为 时,四边形BEHC为菱形.
相关试题

