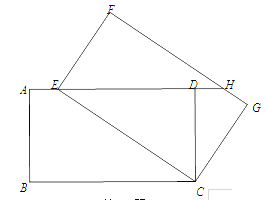
【题目】如图，将矩形ABCD绕点C旋转得到矩形FECG，点E在AD上，延长ED交FG于点H．

（1）求证：△EDC≌△HFE；

（2）连接BE、CH．

①四边形BEHC是怎样的特殊四边形？证明你的结论．

②当AB与BC的比值为 时，四边形BEHC为菱形．

参考答案：

【答案】（1）四边形BEHC为平行四边形，证明见解析；（2）

【解析】试题分析：（1）依据旋转的性质,根据AAS即可证得;(2) ①根据一组对边平行且相等的四边形是平行四边形证得四边形BEHC为平行四边形；②四边形BEHC为菱形,则△BEC是等边三角形,从而∠ABE=30°,即可得到AB与BC的比值.

试题解析：

(1) ∵矩形FECG由矩形ABCD旋转得到，

∴FE＝AB＝DC，∠F=∠EDC =90°，FH∥EC，∴∠FHE=∠CED，

∴△EDC≌△HFE；

(2) ①

四边形BEHC为平行四边形

∵△EDC≌△HFE，∴EH＝EC，

∵矩形FECG由矩形ABCD旋转得到，

∴EH＝EC＝BC，EH∥BC，

∴四边形BEHC为平行四边形；

②由旋转得BC=CE

∴四边形BEHC是菱形

∴BE=CE

∴BE=BC=CE

∴△BCE是等边三角形

∴∠CBE=60°,

∵四边形ABCD是矩形

∴∠ABC=90°

∴∠ABE=30°

∵cos∠ABE=

∴cos30°=

∴

∴当AB和BC的比值为时,四边形BEHC为菱形.

关闭