【题目】如图,已知线段AB=20,C是AB上的一点,D为CB上的一点,E为DB的中点,DE=3. ![]()
(1)若CE=8,求AC的长;
(2)若C是AB的中点,求CD的长.
参考答案:
【答案】
(1)解:∵E为DB的中点,
∴BD=DE=3,
∵CE=8,
∴BC=CE+BE=11,
∴AC=AB﹣BC=9
(2)解:∵E为DB的中点,
∴BD=2DE=6,
∵C是AB的中点,
∴BC= ![]() AB=10,
AB=10,
∴CD=BC﹣BD=10﹣6=4
【解析】(1)由E为DB的中点,得到BD=DE=3,根据线段的和差即可得到结论;(2)由E为DB的中点,得到BD=2DE=6,根据C是AB的中点,得到BC= ![]() AB=10,根据线段的和差即可得到结论.
AB=10,根据线段的和差即可得到结论.
【考点精析】掌握两点间的距离是解答本题的根本,需要知道同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算。
(1)解方程: =1﹣
=1﹣ 
(2)先化简,再求值: (9ab2﹣3)+(7a2b﹣2)+2(ab2+1)﹣2a2b,其中a、b满足(a+2)2+|b﹣3|=0.
(9ab2﹣3)+(7a2b﹣2)+2(ab2+1)﹣2a2b,其中a、b满足(a+2)2+|b﹣3|=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2﹣2(m2﹣1)x+3m=0的两个根是互为相反数,则m的值是( )
A. m=±1B. m=﹣1C. m=1D. m=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为一几何体的三视图:
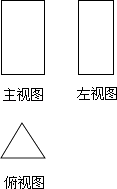
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的高为10cm,正三角形的边长为4cm,求这个几何体的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知A(0,a),B(b,0),且a、b满足a2﹣4a+20=8b﹣b2 .
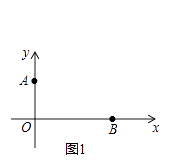
(1)求A、B两点的坐标;
(2)如图2,连接AB,若D(0,﹣6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论;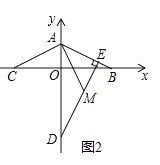
(3)如图3,在(2)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由.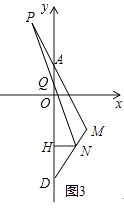
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为2的⊙O中,弦AB=2,⊙O上存在点C,使得弦AC=2
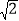 ,则∠BOC=____°.
,则∠BOC=____°.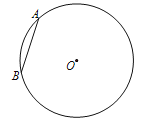
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=13cm,AC=15cm,高AD=12,则BC的长为( )
A.14
B.4
C.14或4
D.以上都不对
相关试题

