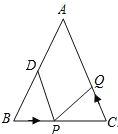
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)如果点![]() 在底边
在底边![]() 上且以
上且以![]() 的速度由
的速度由![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 在腰
在腰![]() 上由
上由![]() 向
向![]() 点运动.
点运动.
①如果点![]() 与点
与点![]() 的运动速度相等,求经过多少秒后
的运动速度相等,求经过多少秒后![]() ;
;
②如果点![]() 与点
与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
(2)若点![]() 以②中的运动速度从点
以②中的运动速度从点![]() 出发,点
出发,点![]() 以
以![]() 速度从点
速度从点![]() 同时出发,都逆时针沿
同时出发,都逆时针沿![]() 三边运动,直接写出当点
三边运动,直接写出当点![]() 与点
与点![]() 第一次相遇时
第一次相遇时![]() 的运动的路程.
的运动的路程.
参考答案:
【答案】(1)①经过1秒;②![]() ;(2)160cm
;(2)160cm
【解析】
(1)①先求得BM=CN=6,MC=BD=10,然后根据等边对等角求得∠B=∠C,最后根据SAS即可证明;
②因为VM≠VN,所以BM≠CN,又∠B=∠C,要使△BMD与△CNM全等,只能BM=CM=8,根据全等得出CN=BD=10,然后根据运动速度求得运动时间,根据时间和CN的长即可求得N的运动速度;
(2)因为VN>VM,只能是点N追上点M,即点N比点M多走AB+AC的路程,据此列出方程,解这个方程即可求得.
(1)①设经过![]() 秒后
秒后![]() ,由题意可得
,由题意可得![]() ,
,
∴![]() ,
,
∴![]() ,在
,在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴经过1秒后![]() ;
;
设经过![]() 秒后
秒后![]() ,记
,记![]() 两点的速度分别为
两点的速度分别为![]() ,
,
∴![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
此时要使![]() 和
和![]() 全等,则
全等,则![]() ,
,
∴![]() ;
;
当![]() 时,若
时,若![]() ,则
,则![]() 中任一边长均比
中任一边长均比![]() 长,
长,
∴![]() 和
和![]() 不可能全等;
不可能全等;
若![]() ,则
,则![]() 中任一边长均比
中任一边长均比![]() 短,
短,
∴![]() 和
和![]() 不可能全等;
不可能全等;
综上所述,当![]() 时,
时,![]() .
.
(2)因为VN>VM,只能是点N追上点M,即点N比点M多走AB+AC的路程,
设经过x秒后M与N第一次相遇,
依题意得![]() x=6x+2×20,
x=6x+2×20,
解得x=![]() (秒)
(秒)
此时点M运动了![]() ×6=160(cm)
×6=160(cm)
故点![]() 与点
与点![]() 第一次相遇时点
第一次相遇时点![]() 运动路径为
运动路径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.

(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC绕点O按顺时针方向旋转90°后的△A2B2C2;
(2)判断△A1B1C1和△A2B2C2是不是成轴对称?如果是,请在图中作出它们的对称轴. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C、D两点将线段AB分为三部分,AC:CD:DB=2:3:4,且AC=4.M是线段AB的中点,N是线段DB的中点.
(1)求线段DB、AB的长.
(2)求线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和CD相交于O点,OE⊥CD,OC平分∠AOF,∠EOF=56°,
(1)求∠BOD的度数;
(2)写出图中所有与∠BOE互余的角,它们分别是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500
 米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
-
科目: 来源: 题型:
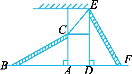
查看答案和解析>>【题目】如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则直线BC与EF的位置关系是____﹒
相关试题

