搜索
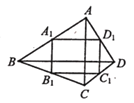
【题目】如图，四边形ABCD的两条对角线AC、BD互相垂直， A1B1C1D1, 是四边形ABCD的中点四边形，如果AC=8, BD=10,那么四边形A1B1C1D1,的面积为_________.
参考答案：
【答案】20
【解析】
此题要能够根据三角形的中位线定理证明四边形A1B1C1D1是矩形，从而根据矩形的面积进行计算．
解：∵A1，B1，C1，D1是四边形ABCD的中点四边形，且AC=8，BD=10
∴A1D1是△ABD的中位线
∴A1D1=0.5BD=0.5×10=5
同理可得A1B1=0.5AC=4
根据三角形的中位线定理，可以证明四边形A1B1C1D1是矩形
那么四边形A1B1C1D1的面积为A1D1×A1B1=5×4=20，故答案为：20.
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据研究弹簧长度与重物重量的实验表格，下列说法错误的是（ ）
A. 自变量是重物重量x，因变量是弹簧长度yB. 弹簧原长8cm
C. 重物重量每增加1kg，弹簧长度伸长4cmD. 当悬挂重物重量为6kg时，弹簧伸长12cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )
A.
B. 
C. 3 D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，AB=12，点E在边CD上，且BG=CG，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF.下列结论：①△ABG≌△AFG；②∠EAG=450；③CE=2DE；④AG∥CF；⑤S△FGC=
.其中正确结论的个数是（ ）
A. 2个 B. 3个 C. 4个 D. 5个
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于每个正整数
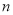，设
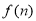表示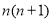
的末位数字．例如：
（
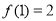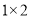的末位数字），
（
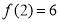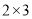的末位数字），
（
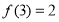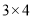的末位数字），…则
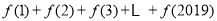的值为（ ）A.4040B.4038C.0D.4042
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AB＝8，AD＝4，点E、F分别在线段AD、AB上，将△AEF沿EF翻折，使得点A落在矩形ABCD内部的P点，连接PD，当△PDE是等边三角形时，BF的长为_____．
-
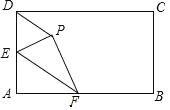
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，G是BC的中点，过A、D、G三点的圆O与边AB、CD分别交于点E、点F，给出下列说法：（1）AC与BD的交点是圆O的圆心；（2）AF与DE的交点是圆O的圆心；（3）BC与圆O相切，其中正确说法的个数是（ ）
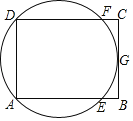
A. 0 B. 1 C. 2 D. 3
相关试题
