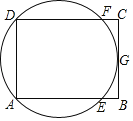
【题目】如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是( )
A. 0 B. 1 C. 2 D. 3
参考答案:
【答案】C
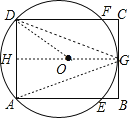
【解析】连接DG、AG,作GH⊥AD于H,连接OD,如图,先确定AG=DG,则GH垂直平分AD,则可判断点O在HG上,再根据HG⊥BC可判定BC与圆O相切;接着利用OG=OD可判断圆心O不是AC与BD的交点;然后根据四边形AEFD为⊙O的内接矩形可判断AF与DE的交点是圆O的圆心.
连接DG、AG,作GH⊥AD于H,连接OD,如图,
∵G是BC的中点,
∴AG=DG,
∴GH垂直平分AD,
∴点O在HG上,
∵AD∥BC,
∴HG⊥BC,
∴BC与圆O相切;
∵OG=OD,
∴点O不是HG的中点,
∴圆心O不是AC与BD的交点;
而四边形AEFD为⊙O的内接矩形,
∴AF与DE的交点是圆O的圆心;
∴(1)错误,(2)(3)正确.
故选:C.
-
科目: 来源: 题型:
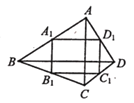
查看答案和解析>>【题目】如图,四边形ABCD的两条对角线AC、BD互相垂直, A1B1C1D1, 是四边形ABCD的中点四边形,如果AC=8, BD=10,那么四边形A1B1C1D1,的面积为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于每个正整数
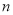 ,设
,设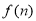 表示
表示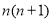 的末位数字.例如:
的末位数字.例如: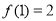 (
(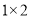 的末位数字),
的末位数字),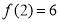 (
(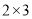 的末位数字),
的末位数字),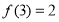 (
(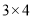 的末位数字),…则
的末位数字),…则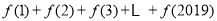 的值为( )
的值为( )A.4040B.4038C.0D.4042
-
科目: 来源: 题型:
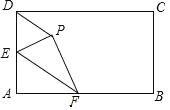
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,AD=4,点E、F分别在线段AD、AB上,将△AEF沿EF翻折,使得点A落在矩形ABCD内部的P点,连接PD,当△PDE是等边三角形时,BF的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两摞规格完全相同的课本整齐叠放在桌子上,请根据图中所给出的数据信息,回答下列问题:
(1)每本课本的厚度为
 ;
;(2)若有一摞上述规格的课本
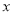 本,整齐叠放在桌子上,请用含
本,整齐叠放在桌子上,请用含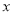 的代数式表示出这一摞数学课本的顶部距离地面的高度为( )
的代数式表示出这一摞数学课本的顶部距离地面的高度为( ) ;
;(3)当
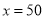 时,若从中取走15本,求余下的课本的顶部距离地面的高度.
时,若从中取走15本,求余下的课本的顶部距离地面的高度.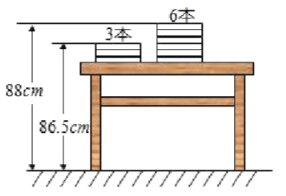
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=10,AC=2
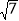 ,∠B=30°,则△ABC的面积等于_____.
,∠B=30°,则△ABC的面积等于_____. -
科目: 来源: 题型:
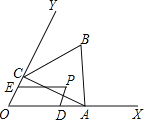
查看答案和解析>>【题目】如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是_____.
相关试题

