【题目】为提供节约用水,某市按如下规定每月收取水费,若一户居民每月用水不超过20立方米,则每立方米按3元收费;若超过20立方米,前20立方米收费标准不变,超过部分每立方米按5元收费,若某户居民某月用水![]() 立方米.
立方米.
(1)试用含![]() (
(![]() >20)的代数式表示这户居民该月应缴的水费.
>20)的代数式表示这户居民该月应缴的水费.
(2)已知该市小李家1月份用水13立方米,2月份用水22立方米,3月份用水17立方米,求他家这三个月应缴纳水费多少元?
参考答案:
【答案】(1)5x-40;(2)160.
【解析】
(1)分别按照:水不超过20立方米,则每立方米按3元收费;超过20立方米,前20立方米收费标准不变,超过部分每立方米按5元收费两种方式列出代数式即可;
(2)把不同数值代入(1)中的代数式求得答案即可.
(1)当x≤20时,该月应缴的水费时3x元;
当x>20时,该月应缴的水费时3×20+5(x20)=(5x40)元;
(2)当x=13,x=22,x=17时,
3×13+5×2240+3×17=160元
答:他家一季度应缴纳水费160元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)如果点P到点A,点B的距离相等,那么x=______;
(2)当x=______时,点P到点A,点B的距离之和是6;
(3)若点P到点A,点B的距离之和最小,则x的取值范围是______;
(4)在数轴上,点M,N表示的数分别为x
 ,x
,x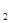 ,我们把x
,我们把x ,x
,x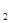 之差的绝对值叫做点M,N之间的距离,即MN="|" x
之差的绝对值叫做点M,N之间的距离,即MN="|" x -x
-x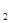 |.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等.
|.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个被等分成了3个相同扇形的圆形转盘,3个扇形分别标有数字1、3、6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停止在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).
(1)请用画树形图或列表的方法(只选其中一种),表示出分别转动转盘两次转盘自由停止后,指针所指扇形数字的所有结果;
(2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料
材料1:对称,也许是中国人最喜欢的。建筑师梁思成曾说过:“无论东方、西方,再没有一个民族对中轴对称线如此钟爱与恪守。”放眼中国的建筑,无论是宫殿、庙宇、亭台、楼阁、园林无不有着对称之美。数学世界也里有一些正整数你无论从左往右看,还是从右往左看,数字都是完全一样的,例如:11、101、2332、1234321、…,像这样的数我们叫它“对称数”.
材料2:如果一个三位数
 ,满足a+b+c=8,我们就称这个三位数为“发财数”.
,满足a+b+c=8,我们就称这个三位数为“发财数”.(1)请直接写出既是“对称数”又是“发财数”的所有三位数;
(2)一个三位“对称数”十位数字为7,它的各数位上的数字之和是一个自然数的平方,求这个三位数(请写出必要的推理过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
甲
85
95
95
乙
95
85
95
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图象经过A(2,0),B(0,-6)两点.
的图象经过A(2,0),B(0,-6)两点.(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
(3)在x轴上是否存在一点P,使△ABP为等腰三角形,若存在,求出P的坐标,若不存在,说明理由.

相关试题

