【题目】
(1)如果点P到点A,点B的距离相等,那么x=______;
(2)当x=______时,点P到点A,点B的距离之和是6;
(3)若点P到点A,点B的距离之和最小,则x的取值范围是______;
(4)在数轴上,点M,N表示的数分别为x![]() ,x
,x![]() ,我们把x
,我们把x![]() ,x
,x![]() 之差的绝对值叫做点M,N之间的距离,即MN="|" x
之差的绝对值叫做点M,N之间的距离,即MN="|" x![]() -x
-x![]() |.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等.
|.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等.
参考答案:
【答案】(1)-1;(2)-4或2;(3)![]() ;(4)
;(4)![]() 或2.
或2.
【解析】试题分析:(1)根据题意列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值;
的值;
根据题意列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值;
的值;
(3)点P到点A,点B的距离之和最小,则点P在线段AB上,求出![]() 的取值范围即可;
的取值范围即可;
(4)设![]() 秒时点P到点E,点F的距离相等,根据题意列出关于
秒时点P到点E,点F的距离相等,根据题意列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值.
的值.
试题解析:(1)根据题意得,![]()
![]()
根据题意得,![]() 解得
解得![]() 或
或![]() ;
;
点P到点A,点B的距离之和最小,点P在线段AB上,则![]() 的取值范围为
的取值范围为![]() ;
;
设![]() 秒时点P到点E,点F的距离相等,根据题意得:
秒时点P到点E,点F的距离相等,根据题意得:![]() 解得:
解得:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=6,AN=2,∠BAC的平分线交BC于点D,M是AD上的动点,则BM+MN的最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细观察下面的日历,回答下列问题:
(1)任意用正方形框圈出四个日期,如果正方形框中的第一个数(左上角的数)为
 ,用代数式表示正方形框中的四个数的和;
,用代数式表示正方形框中的四个数的和;(2)若将正方形框上下左右移动,可框住另外的四个数,这四个数的和能等于
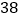 吗?如果能,依次写出这四个数;如果不能,请说明理由.
吗?如果能,依次写出这四个数;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
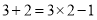 ,
,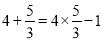 ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 成立的一对有理数
成立的一对有理数 为“理想有理数对”,记为
为“理想有理数对”,记为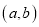 ,如:数对
,如:数对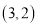 、
、 都是“理想有理数对”.
都是“理想有理数对”.(1)数对
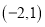 、
、 中是“理想有理数对”的是______;
中是“理想有理数对”的是______;(2)若
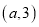 是“理想有理数对”,求a的值;
是“理想有理数对”,求a的值;(3)若
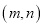 是“理想有理数对”,则
是“理想有理数对”,则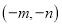 ______“理想有理数对”(填“是”、“不是”或“不确定”);
______“理想有理数对”(填“是”、“不是”或“不确定”);(4)请再写出一对符合条件的“理想有理数对”.(不能与题目中已有的数对重复).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个被等分成了3个相同扇形的圆形转盘,3个扇形分别标有数字1、3、6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停止在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).
(1)请用画树形图或列表的方法(只选其中一种),表示出分别转动转盘两次转盘自由停止后,指针所指扇形数字的所有结果;
(2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为提供节约用水,某市按如下规定每月收取水费,若一户居民每月用水不超过20立方米,则每立方米按3元收费;若超过20立方米,前20立方米收费标准不变,超过部分每立方米按5元收费,若某户居民某月用水
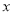 立方米.
立方米.(1)试用含
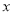 (
(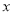 >20)的代数式表示这户居民该月应缴的水费.
>20)的代数式表示这户居民该月应缴的水费.(2)已知该市小李家1月份用水13立方米,2月份用水22立方米,3月份用水17立方米,求他家这三个月应缴纳水费多少元?
相关试题

