【题目】如图所示,在△ABC中,AB=3,AC=4,BC=5,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
(1)求证:四边形DAEF是平行四边形;
(2)求四边形DAEF的面积.

参考答案:
【答案】(1)见解析;(2)6
【解析】
(1)先根据等边三角形的性质和SAS证明△BDF≌△BAC,可得DF=AC,进而可得DF=AE,同理可得DA=EF,于是可根据两组对边分别相等的四边形是平行边形来证明结论;
(2)先证明△ABC为直角三角形,进而可求得∠DAE=150°,进一步可得∠FDA=30°,过F作FM⊥AD,然后利用30°角的直角三角形的性质可求得FM的长,进而可得结果.
(1)证明:∵等边△BCF和等边△ABD,
∴BF=BC,BD=BA,∠FBC=∠DBA=60°,
又∵∠DBF=60°﹣∠ABF,∠ABC=60°﹣∠ABF,
∴∠DBF=∠ABC.
∴△BDF≌△BAC(SAS).
∴DF=AC.
∵在等边△ACE中,AC=AE,
∴DF=AE.
同理DA=EF.
∴四边形DAEF是平行四边形;
(2)解:∵AB=3,AC=4,BC=5,
∴AB2+AC2=32+42=52=BC2,
∴△ABC为直角三角形,
∴∠BAC=90°,
又∵∠DAB=∠EAC=60°,
∴∠DAE=360°﹣90°﹣60°﹣60°=150°,
∴∠FDA=30°,
如图,过F作FM⊥AD于点M,

则FM=![]() FD=
FD=![]() AE=
AE=![]() AC=2,
AC=2,
∴S四边形DAEF=ADFM=3×2=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点
,把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点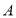 处,并按
处,并按 的规律紧绕在四边形
的规律紧绕在四边形 的边上,则细线另一端所在位置的点的坐标是( )
的边上,则细线另一端所在位置的点的坐标是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
组别
捐款额(x)元
户数
A
1≤x<50
a
B
50≤x<100
10
C
100≤x<150
D
150≤x<200
E
x≥200
请结合以上信息解答下列问题.

(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC:
(1)求作△ABC的内切圆⊙O,与边AB、BC、AC分别相切于点D、E、F;
(2)若AB=6,BC=8,AC=12,求AD、BE、CF的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=
 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
 的坐标分别是
的坐标分别是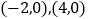 ,现同时将点
,现同时将点 分别向上平移2个单位长度,再向右平移2个单位长度,得到
分别向上平移2个单位长度,再向右平移2个单位长度,得到 的对应点
的对应点 .连接
.连接 .
.(1)写出点
 的坐标并求出四边形
的坐标并求出四边形 的面积.
的面积.(2)在
 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 的面积是
的面积是 面积的2倍?若存在,请求出点
面积的2倍?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(3)若点
 是直线
是直线 上一个动点,连接
上一个动点,连接 ,当点
,当点 在直线
在直线 上运动时,请直接写出
上运动时,请直接写出 与
与 的数量关系.
的数量关系.
相关试题

