搜索
【题目】已知△ABC的三边a、b、c满足 
=0，求最长边上的高h．
参考答案：
【答案】解：由题意，得： 
，2b﹣12=0，10﹣c=0，
∴a=8，b=6，c=10，
∵a2+b2=64+36=100=c2，
∴△ABC为Rt△ABC，且∠C=90°，
∵ 
ch= ab，
∴h=4.8
【解析】根据绝对值，偶次方及算术平方根的非负性知几个非负数的和为零，则这几个数都为零，从而得出a,b,c的值，然后根据勾股定理的逆定理判断出△ABC为Rt△ABC，且∠C=90°，根据直角三角形面积的计算方法得出答案。
【考点精析】通过灵活运用勾股定理的逆定理，掌握如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的一元二次方程x2+3x=0的根的说法正确的是（ ）
A.没有实数根
B.只有一个实数根
C.有两个相等的实数根
D.有两个不相等的实数根 -
科目： 来源： 题型：
查看答案和解析>>【题目】计算题
（1）计算：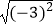
+ 
×（﹣ 
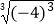）2
（2）求x的值：（x﹣2）3=﹣27． -
科目： 来源： 题型：
查看答案和解析>>【题目】某班组织班团活动，班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品，已知笔记本2元/本，中性笔1元/支，且每种奖品至少买1件．
（1）若设购买笔记本x本，中性笔y支，写出y与x之间的关系式；
（2）有多少种购买方案？请列举所有可能的结果；
（3）从上述方案中任选一种方案购买，求买到的中性笔与笔记本数量相等的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球（除颜色不同外其余都相同），其中红球有2个，黄球有1个，从中任意捧出1球是红球的概率为
（1）试求袋中绿球的个数；
（2）第1次从袋中任意摸出l球（不放回），第2次再任意摸出1球，请你用画树状图或列表格的方法，求两次都摸到红球的概率.
-
科目： 来源： 题型：
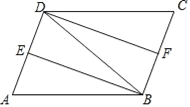
查看答案和解析>>【题目】如图，在ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．
（1）求证：△ABE≌△CDF；
（2）若AB=DB，猜想：四边形DFBE是什么特殊的四边形？并说明理由．
-
科目： 来源： 题型：
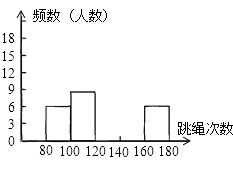
查看答案和解析>>【题目】为了进一步了解九年级500名学生的身体素质情况，体育老师对九年级（1）班50名学生进行一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图如下所示：
组别
次数x
频数（人数）
第l组
80≤x＜100
6
第2组
100≤x＜120
8
第3组
120≤x＜140
a
第4组
140≤x＜160
18
第5组
160≤x＜180
6
请结合图表完成下列问题：
（1）表中的a=，次数在140≤x＜160这组的频率为；
（2）请把频数分布直方图补充完整；
（3）若九年级学生一分钟跳绳次数（x）达标要求是：x＜120不合格；x≥120为合格，则这个年级合格的学生有人．
相关试题
